Анна Малкова
Многие старшеклассники считают, что геометрия сложнее алгебры. «В алгебре все просто, - говорят они. – Есть способы решения уравнений. Есть типы задач – на движение, на работу, на проценты – и для каждой свои приемы решения. А задачи геометрии друг на друга не похожи».
Так ли это? Может быть, и в планиметрии есть схемы, на которых строится множество задач?
Да, есть. Я называю их «классические схемы планиметрии». Учимся узнавать их и использовать в задачах! И возможно, что на ЕГЭ вам встретится задача, «ключиком» к которой будет одна из этих схем. Конечно, на ЕГЭ эти утверждения надо доказывать.
Вот 5 полезных схем для решения задач по планиметрии.
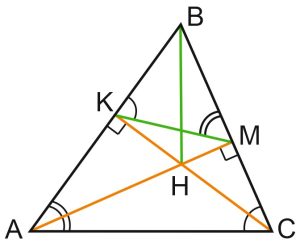
Схема 1. Высоты треугольника. Свойства ортоцентра.
В треугольнике \(ABC\) проведены высоты \(AM\) и \(CK.\)
\(H\) – точка пересечения высот треугольника (ортоцентр), \(H=AM∩CK.\)
Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.
1. Треугольники \(MBK\) и \(ABC\) подобны, причем коэффициент подобия \(k=cosB\), если \(\angle B< 90^{\circ}\), и \(k=|cosB|\), если \(\angle B > 90^{\circ}.\)
2. Четырехугольник \(AKMC\) можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
3. Четырехугольник \(BKMH\) также можно вписать в окружность.
4. Радиусы окружностей, описанных вокруг треугольников \(ABC, \ AHC, \ BHC, \ ABH\), равны.
5. \(BH=2R| cosB|\), где \(R\) – радиус описанной окружности \(\triangle ABC.\)
Докажем эти факты по порядку.
1) Заметим, что на рисунке есть подобные треугольники. Это \(ABM\) и \(CBK\), прямоугольные треугольники с общим углом \(B\), и они подобны по двум углам:
\(\triangle ABM ∼ \triangle CBK\Rightarrow \displaystyle\frac{BM}{BK}=\frac{AB}{BC}\Rightarrow \frac{BM}{AB}=\frac{BK}{BC}.\)
Мы получили, что в треугольниках \(MBK\) и \(ABC\) стороны, прилежащие к углу \(B\), пропорциональны.
Получаем, что \(\triangle MBK∼ \triangle ABC\) по углу и двум сторонам.
2) Докажем, что вокруг четырехугольника \(AKMC\) можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника \(AKMC\) были равны \(180 ^{\circ}.\)
Пусть \(\angle ACB= \angle BKM=\gamma\) (поскольку треугольники \(MBK\) и \(ABC\) подобны), тогда \(\angle ACB= \angle BKM=\gamma\) – как смежный с углом \(BKM\).
Получили, что \(\angle AKM + \angle ACM=180 ^{\circ}\), и это значит, что четырехугольник \(AKMC\) можно вписать в окружность.
3) Рассмотрим четырехугольник \(KBMH\). Его противоположные углы \(BKH\) и \(BMH\) – прямые, их сумма равна \(180 ^{\circ}\), и значит, четырехугольник \(KBMH\) можно вписать в окружность.
4) По теореме синусов, радиус окружности, описанной вокруг треугольника \(ABC, \ R_{\triangle ABC}=\displaystyle \frac{AC}{2sin \angle ABC}.\)
Радиус окружности, описанной вокруг треугольника \(AHC, \ R_{\triangle AHC}=\displaystyle \frac{AC}{2sin \angle AHC}.\)
Мы помним, что \(sin( 180 ^{\circ}-\alpha)=sin\alpha\). Значит, синусы углов \(ABC\) и \(AHC\) равны, и радиусы окружностей, описанных вокруг треугольников \(ABC\) и \(AHC\) равны.
5) Докажем, что \(BH=2R|cosB|\), где \(R\) – радиус описанной окружности \(\triangle ABC.\)
Поскольку четырехугольник \(KBMH\) можно вписать в окружность и углы \(BKH\) и \(BMH\) – прямые, отрезок \(BH\) является диаметром этой окружности.
Треугольник \(MBK\) также вписан в эту окружность, и по теореме синусов, \(BH= \displaystyle \frac{MK}{sin \angle ABC}.\)
Диаметр окружности, описанной вокруг треугольника \(ABC\), равен \(\displaystyle \frac{AC}{sin \angle ABC}.\)
Поскольку треугольники \(MBK\) и \(ABC\) подобны, отношение диаметров описанных вокруг них окружностей равно \(|cosB|.\)
Получили, что \(BH=2R|cosB|.\)
Схема 2. Пусть луч \(MA\) пересекает окружность в точках \(A\) и \(B\), а луч \(MD\) – в точках \(C\) и \(D\), причем \(MA \gt MB\), \(MD \gt MC\). Тогда треугольники \(BMC\) и \(DMA\) подобны.
\(\triangle BMC ∼ \triangle DMA.\)
Пусть угол \(BAD\) равен \(α\). Четырехугольник \(ABCD\) вписан в окружность, поэтому угол \(BCD\) равен \(180° - α\). Угол \(BCM\) – смежный с углом \(BCD\), и значит, \(∠BCM= ∠BAD = α\), треугольники \(BMC\) и \(DMA\) подобны по двум углам.
Схема 3. У треугольников \(ABC\) и \(AMC\) сторона \(AC\) – общая, угол \(B\) равен углу \(M\), причем точки \(B\) и \(M\) лежат по одну сторону от прямой \(AC\). Тогда точки \(A, \; B, \; C, \; M\) лежат на одной окружности.
В самом деле: по теореме синусов, радиус окружности, описанной вокруг треугольника \(ABC\), равен радиусу окружности, описанной вокруг треугольника \(AMC\) и равен \(\displaystyle \frac{AC}{2sin \varphi}.\) А это значит, что точки \(A, B, M\) и \(C\) лежат на одной окружности.
Можно доказать и более общее утверждение: геометрическое место точек \(M\), из которых отрезок \(AB\) виден под данным углом, есть две дуги равных окружностей с общей хордой \(AB\), без точек \(A\) и \(B.\)
Схема 4. У треугольников \(ABC\) и \(AMC\) сторона \(AC\) – общая, углы \(B\) и \(M\) – прямые. Тогда точки \(A, \ B, \ C, \ M\) лежат на окружности, радиус которой равен половине \(AC.\)
Иначе говоря, геометрическое место точек \(M\), из которых отрезок \(AB\) виден под прямым углом, есть окружность с диаметром \(AC\) без точек \(A\) и \(C.\)
Как и в предыдущей схеме, воспользуемся теоремой синусов.
\(\displaystyle \frac{AC}{sin \angle B}=\frac{AC}{sin \angle M}=AC=2R\), где \(R\) – радиус окружности, описанной вокруг треугольника \(ABC\), а также вокруг треугольника \(AMC\). Это значит, что точки \(A, \ B, \ M\) и \(C\) лежат на окружности, центром которой является середина \(AC.\)
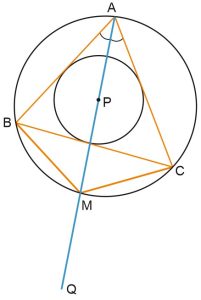
Схема 5. Лемма о трезубце (трилистнике)
Пусть \(P\) – центр вписанной окружности треугольника \(ABC, \ Q\) – центр его вневписанной окружности, касающейся стороны \(BC.\)
Точка пересечения биссектрисы угла \(A\) треугольника \(ABC\) с его описанной окружностью равноудалена от точек \(B, \ C, \ P, \ Q.\) Эта схема называется также теоремой о трилистнике.
Дан треугольник \(ABC, \ AM\) – биссектриса угла \(A, \ P\) – центр вписанной окружности треугольника \(ABC, \ Q\) – центр его вневписанной окружности (которая касается стороны \(BC\) и продолжений сторон \(AB\) и \(AC\), \(M\) – точка пересечения биссектрисы угла \(A\) и описанной окружности треугольника \(ABC\). Докажем, что \(MP = MB = MC.\)
Видите на рисунке «трезубец» (или «трилистник»), состоящий из отрезков \(MP, \ MB, \ MC, \ MQ\)?
Докажем сначала, что \(MB = MC = MP.\)
Вписанные углы \(BAM\) и \(BCM\) опираются на дугу \(BM\), следовательно, они равны.
Аналогично, вписанные углы \(CAM\) и \(CBM\) опираются на дугу \(CM\), и они тоже равны.
\(\angle BAM=\angle CAM\), поскольку \(AM\) – биссектриса угла \(BAC.\)
Следовательно, \(\angle BCM=\angle BAM=\angle CAM=\angle CBM= \alpha\) и треугольник \(BMC\) – равнобедренный, \(BM = CM.\)
Точка \(P\) – центр вписанной окружности треугольника \(ABC\). Значит, \(P\) – точка пересечения биссектрис треугольника \(ABC\), и тогда \(BP\) и \(CP\) – биссектрисы его углов \(ABC\) и \(ACB\) соответственно.
Пусть \(\angle BAC=2\alpha, \ \angle ABC=2\beta , \ \angle ACB=2\gamma.\)
Сумма углов треугольника \(ABC\) равна \(180^{\circ}\), значит, \(2\alpha +2\beta +2\gamma =180^{\circ}.\)
В треугольнике \(BMP:\)
\(\angle PMB=\angle ACB=2\gamma,\)
\(\angle PBM=\alpha+\beta.\)
Тогда \(\angle BPM=\alpha+\beta=\angle PBM\), треугольник \(BMP\) равнобедренный, \(BM = PM\). Значит, точка \(M\) равноудалена от точек \(B, \ C\) и \(P\). Аналогично доказывается, что \(MQ = BM = CM = PM.\)
Схема 6. Теорема Менелая и теорема Чевы.
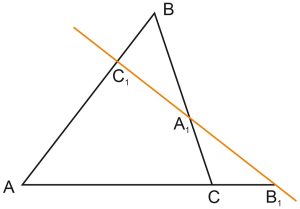
Теорема Менелая
Пусть прямая пересекает произвольный треугольник \(ABC\), причем \(C_1\) – точка ее пересечения со стороной \(AB, A_1\) – точка ее пересечения со стороной \(BC,\) и \(B_1\) – точка ее пересечения с продолжением стороны \(AC.\)
\(\displaystyle \frac{AC_1}{C_1B} \cdot \frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A} = 1.\)
Как это запомнить? Сначала рисуем треугольник \(ABC.\) Затем прямую, пересекающую две его стороны и продолжение третьей. На этой прямой лежат точки \(C_1, \ A_1\) и \(B_1,\) причем на стороне \(AB\) должна лежать точка \(C_1,\) на стороне \(BC\) – точка \(A_1\) и на продолжении \(AC\) – точка \(B_1.\)
Затем записываем равенство так, как будто «обходим» весь треугольник \(ABC,\) от точки \(A\) к точкам \(B\) и \(C,\) и затем возвращаемся в точку \(A.\) Но по дороге нам встречаются точки \(C_1, \ A_1\) и \(B_1\) – их тоже включаем в формулу.
Один из учащихся нашей ЕГЭ-Студии предложил такое мнемоническое правило: пусть точки \(A, \ B\) и \(C\) – это города, а точки \(C_1, \ A_1\) и \(B_1\) – заправки, где можно пополнить запас бензина. Тогда правило звучит так: «Едем из города в город, заезжаем на заправку!» Возможно, вы придумаете свое правило : -)
В некоторых задачах полезна обратная теорема Менелая.
Пусть дан треугольник \(ABC.\) Предположим, что точка \(C_1\) лежит на стороне \(AB,\) точка \(A_1\) лежит на стороне \(BC,\) а точка \(B_1\) лежит на продолжении стороны \(AC,\) причём про эти точки известно, что
\(\displaystyle \frac{AC_1}{C_1B} \cdot \frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A} = 1.\)
Тогда эти точки лежат на одной прямой.
Как правило, не так-то просто бывает доказать, что три точки лежат на одной прямой. Обычно мы используем для доказательства такого факта косвенные методы. Например, если для точек \(A, \ B\) и \(C\) выполняется равенство: \(AB + BC = AC\) – то это означает, что точка \(B\) лежит на отрезке \(AC.\) Или, если нам удается доказать, что угол \(ABC\) – развернутый, это и будет означать, что точки \(A, \ B\) и \(C\) лежат на одной прямой. Обратная теорема Менелая дает еще один способ доказательства того, что три точки – в данном случае \(A_1, \ B_1\) и \(C_1\) – лежат на одной прямой.
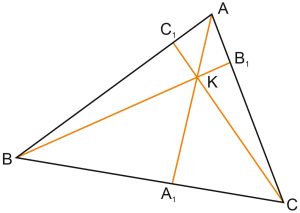
Теорема Чевы
Пусть точки \(A_1, B_1\) и \(C_1\) лежат соответственно на сторонах \(BC, \ AC\) и \(AB\) треугольника \(ABC\) причем отрезки \(A A_1, \ BB_1\) и \(C C_1\) пересекаются в одной точке.
В этом случае выполняется равенство: \(\displaystyle \frac{AC_1}{C_1B} \cdot \frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A} = 1.\)
Пусть точки \(A_1, \ B_1, \ C_1\) лежат соответственно на сторонах \(BC, \ AC\) и \(AB\) треугольника \(ABC,\) причём
\(\displaystyle \frac{AC_1}{C_1B} \cdot \frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A} = 1.\)
Тогда отрезки \(A A_1, \ BB_1\) и \(C C_1\) пересекаются в одной точке.
И несколько лайфхаков для сдающих ЕГЭ.
1) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Менелая и другую экзотику – вам это и не понадобится. Только то, что есть в нашем Супер-Справочнике. И полезные факты. Зато знать это надо наизусть.
2) Когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур – у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. В каких формулах он встречается? – Правильно, в теореме синусов и в одной из формул для площади треугольника.
3) Есть такие теоремы, которые вроде и входят в школьную программу – а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы треугольника. А вы их знаете?
4) Как научиться решать задачи по геометрии? Если у вас маловато опыта – не стоит начинать с реальных задач ЕГЭ. Сначала – задачи на доказательство. Тем более что в реальной задаче 16 из варианта ЕГЭ первый пункт – доказательство.
5) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. А это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б).
6) Среди стратегий подготовки к ЕГЭ есть эффективные. А есть откровенно проигрышные.
Пример плохой стратегии – когда старшеклассник принимает решение заниматься только алгеброй и считает планиметрию и тем более стереометрию слишком сложными для себя. И вот на ЕГЭ попадается сложное неравенство или «экономическая» задача. И всё, баллов не хватает! Тех самых баллов за планиметрию и стереометрию, которые можно было взять, не хватает для поступления!
Чтобы такого не случилось – занимаемся планиметрией как можно больше.
7) Стоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.