Центр подготовки к ЕГЭ > Материалы для подготовки к ЕГЭ и ОГЭ > Что такое функция

Что такое функция

Понятие функции – одно из основных в математике.

На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.

Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.

\(1.\) Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.

Любой физический закон, любая формула отражает такую взаимосвязь величин. Например, формула \(\smash{p=\rho gh}\) – это зависимость давления жидкости \(\smash{p}\) от глубины \(h\).

Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.

Знакомое вам обозначение \(y=f \left( x \right)\) как раз и выражает идею такой зависимости одной величины от другой. Величина \(y\) зависит от величины \(x\) по определенному закону, или правилу, обозначаемому \(f\).

Другими словами: меняем \(x\) (независимую переменную, или аргумент) – и по определенному правилу меняется \(y\).

Совсем необязательно обозначать переменные \(x\) и \(y\). Например, \(L\left( t \right) = L_0 \left( 1+ \alpha t \right) \) – зависимость длины \(L\) от температуры \(t\), то есть закон теплового расширения. Сама запись \(L\left( t \right)\) означает, что величина \(L\) зависит от \(t\).

\(2.\) Можно дать и другое определение.

Функция – это определенное действие над переменной.

Это означает, что мы берем величину \(x\), делаем с ней определенное действие (например, возводим в квадрат или вычисляем ее логарифм) – и получаем величину \(y\).

В технической литературе встречается определение функции как устройства, на вход которого подается \(x\), а на выходе получается \(y\).

Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.

\(3.\) Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.

Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Например, функция \(y=2x\) каждому действительному числу \(x\) ставит в соответствие число в два раза большее, чем \(x\).

Повторим еще раз: каждому элементу множества \(X\) по определенному правилу мы ставим в соответствие элемент множества \(Y\). Множество \(X\) называется областью определения функции. Множество \(Y\) – областью значений.

Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.

Рассмотрим в качестве примера соответствие между двумя множествами – гражданами России, у которых есть паспорта, и номерами их паспортов. Ясно, что это соответствие взаимно-однозначное – у каждого гражданина только один российский паспорт. И наоборот – по номеру паспорта можно найти человека.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция \(y=3x+2\). Каждому значению \(x\) соответствует одно и только одно значение \(y\). И наоборот – зная \(y\), можно однозначно найти \(x\).

\(x\)	\(-3\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)
\(y=3x+2\)	\(-7\)	\(-4\)	\(-1\)	\(2\)	\(5\)	\(8\)

Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:

Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились и Сергей, и Олег.

Пример такого соответствия в математике – функция \(y=x^2\). Один и тот же элемент второго множества \(y=4\) соответствует двум разным элементам первого множества: \(x=2\) и \(x=-2\).

А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:

Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.

Очень сложно было бы описать такое соответствие математически, не правда ли?

Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?

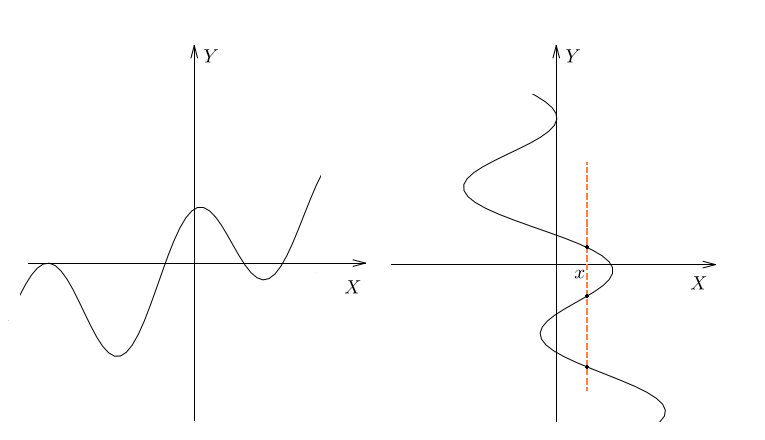
Ответ очевиден. Первая кривая – это график некоторой функции, а вторая – нет. Ведь на ней есть точки, где каждому значению \(x\) соответствует не одно, а целых три значения \(y\).

Перечислим способы задания функции.

\(1.\) С помощью формулы. Это удобный и привычный для нас способ. Например:

\(y=\cos x;\)

\(y=x^3-2x^2;\)

\(z=f\left( t \right);\)

\(L\left( t \right) = L_0 \left( 1+ \alpha t \right). \)

Это примеры функций, заданных формулами.

\(2.\) Графический способ. Он является самым наглядным. На графике сразу видно все – возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума. В следующей статье будет рассказано об исследовании функции с помощью графика.

К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.

\(3.\) С помощью таблицы. С этого способа вы когда-то начинали изучение темы «Функция» - строили таблицу и только после этого – график. А при экспериментальном исследовании какой-либо новой закономерности, когда еще неизвестны ни формула, ни график, этот способ будет единственно возможным.

\(4.\) С помощью описания. Бывает, что на разных участках функция задается разными формулами. Известная вам функция \(y=|x|\) задается описанием:

\(|x|=
\left\{\begin{matrix}
x, x\geq 0, \\ -x, x < 0.
\end{matrix}\right. \)

Даже в первой части ЕГЭ по математике есть задачи на понимание определения функции.

Задание 1. Найдите \(\displaystyle \frac{g(5-x)}{g(5+x)},\) если \(g(x)=\sqrt[9]{x(10-x)},\) при \(|x| \neq 5.\)

Что такое \(g(x)\)? Это функция, каждому числу \(x\) ставящая в соответствие число \(\sqrt[9]{x\cdot(10-x)}.\) Например, \(g(0)=0; \)

\(g(1)=\sqrt[9]{1\cdot(10-1)}=\sqrt[9]{9},\)

Тогда \(g(5-x)=\sqrt[9]{(5-x)(10-5+x)}=\sqrt[9]{(5-x)(5+x)},\)

\(g(5+x)=\sqrt[9]{(5+x)(10-5-x)}=\sqrt[9]{(5+x)(5-x)}\)

Заметим, что

\(g(5-x)=g(5+x).\)

Значит, при \(|x| \neq 5, \displaystyle ~\frac{g(5-x)}{g(5+x)}=1.\)

Задание 2. Найдите \(\displaystyle \frac{p(b)}{p(\frac{1}{b})},\) если \(p(b)=\left(b-\displaystyle \frac{9}{b}\right)\left(-9b+\displaystyle \frac{1}{b}\right),\) при \(b \neq 0.\)

\(p(b)=\left(b-\displaystyle \frac{9}{b}\right)\left(-9b+\displaystyle \frac{1}{b}\right) -\) функция, каждому числу \(b\) ставящая в соответствии число

\(\left(b-\displaystyle \frac{9}{b}\right)\left(-9b+\displaystyle \frac{1}{b}\right).\)

Тогда \(b \neq 0\) \(p\left (\displaystyle \frac{1}{b}\right)=\left(\displaystyle \frac{1}{b}-9b\right)\left(\displaystyle -\frac{9}{b}+b\right)=\left(b\displaystyle -\frac{9}{b}\right)\left(-9b+\displaystyle \frac{1}{b}\right)=p(b),\) и значение \(\displaystyle \frac{p(b)}{p(\frac{1}{b})}=1.\)

Задание 3, подготовительная задача. Найдите область определения функции \(f(x)=\sqrt{x+1}+\sqrt{3-x}\)

Очевидно, что оба подкоренных выражения должны быть неотрицательны. Получим систему:

\(
\begin{cases}
x+1 \geqslant 0, \\
3-x \geqslant 0.
\end{cases}
\)

Решая ее, найдем область определения функции: \(x\in [-1;3].\)

Понятие функции – одно из основных в программе математики 10-11 класса. Более того – именно с функций и графиков начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции – это все-таки арифметика. Математика – наука не только о числах, но и о взаимосвязях величин. Функции и графики – универсальный язык, понятный физику и биохимику, астроному, инженеру и экономисту.

В настоящее время в вариантах ЕГЭ появилась задача по теме: Функции и графики. Есть также задачи на темы: точки максимума и минимума, поведение функции.

Тема Функции и графики есть также в вариантах ОГЭ по математике. Разберем реальные задачи ОГЭ и ЕГЭ по этим темам.

Смотри также:

Исследование графика функции

Элементарные функции и их графики

Четные и нечетные функции

Периодические функции

Обратная функция

Преобразование графиков функций

Построение графиков функций

Задачи ЕГЭ по теме: Функции и графики

Задача 1. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Линейная функция задается формулой \(y=kx+b.\)

1) Найдем формулу первой функции, возрастающей. На ее графике выделены точки \((-3;-3)\) и \((-1; 4).\)

Угол наклона этой прямой к оси абсцисс острый, значит \(k>0;\)
\(k=tg\alpha=\displaystyle \frac{7}{2}=3,5.\)

Формула функции: \(y=3,5x+b.\).

Найдем \(b\) и для этого подставим координаты любой из выделенных точек, например, точки с координатами \((-1; 4).\)

\(4=3,5\cdot(-1)+b \Rightarrow b=7,5\)

\(y=3,5x+7,5 -\) это формула возрастающей функции.

2) Найдем уравнение второй линейной функции, убывающей. На ее графике выделены точки \((-4;5)\) и \((-2; 2).\)

Угол наклона этой прямой к оси абсцисс тупой, значит, для нее \(k<0;\)

\(k=tg\alpha=\displaystyle -\frac{3}{2}=-1,5.\)

Уравнение этой прямой имеет вид: \(y=-1,5x+b\).

Найдем \(b\) и для этого подставим координаты любой из выделенных точек, например, точки с координатами \((-2; 2).\)

\(2=-1,5\cdot(-2)+b \Rightarrow b =-1;\)

\(y=-1,5x-1 -\) это формула второй функции, убывающей.

3) Найдем абсциссу точки пересечения графиков функций. Для этого решим уравнение:

\(-1,5x-1=3,5x+7,5; \; ~5x=-8,5; \; ~x=-1,7.\)

Ответ: -1,7.

Задача 2. На рисунке изображен график функции \(f(x)\), определенной на отрезке \([-4,5; 3,5].\) Найдите количество точек максимума функции \(f(x)\) на данном отрезке.

Решение:

Точка максимума – такая внутренняя точка области определения функции, значение функции в которой больше, чем во всех достаточно близких к ней точках (локальная «горка» на графике). Таких точек мы видим три.

Ответ: 3

Задача 3. Графики функций \(y=2x^2-a\) и \(y=b-5x\) пересекаются в точках \(C\) и \(E\), причем абсцисса точки \(C\) положительна. Найдите абсциссу точки \(E\).

Решение:

Найдем сначала значения параметров \(a\) и \(b\).

График функции \(y=2x^2-a\) проходит через точку с координатами \((0; -1).\)

Подставим \(x = 0\) и \(y = -1\) в формулу функции \(y=2x^2-a.\)

Получим: \(a=1.\)

Значит, эта функция задается уравнением \(y=2x^2-1.\)

График функции \(y=b-5x\) проходит через точку \((0; 2),\) значит, \(b=2,\) линейная функция задается уравнением \(y=2-5x.\)

Для точек пересечения графиков этих функций выполняется равенство:

\(2x^2-1=2-5x.\)

Отсюда \(2x^2+5x-3=0.\) Решим это квадратное уравнение.

\( D=25+24=49, \; x=\displaystyle \frac{-5\pm7}{4}, \; x_1=0,5, \; x_2=-3.\)

Так как абсцисса точки \(C\) положительна, она равна \(0,5\). Эта точка пересечения графиков показана на рисунке.
Абсцисса точки \(E\) (находится за пределами рисунка) равна \(-3\).

Ответ: -3.

Задача 4. Графики функций \(f(x)=3(x+1)^2\) и \(g(x)\) пересекаются в точках \(A\) и \(B\). По данным рисунка найдите абсциссу точки \(B\).

Решение:

Запишем формулу функции \(y=g(x).\)

График этой квадратичной функции – парабола \(g(x)=ax^2+bx+c;\)

\(g(-2)=3;\)

\(g(-4)=-5.\)

То есть:

\(
\begin{cases}
a \cdot (-2)^2+b\cdot(-2)+c=3,\\
a\cdot (-4)^2+b\cdot (-4)+c=-5;
\end{cases}
\)

\(
\begin{cases}
4a-2b+c=3, \\
16a-4b+c=-5.
\end{cases}
\)

Вычитаем из первого уравнения второе:

\(-12a+2b=8,\) то есть \(-6a+b=4. \)

Так как \(x=-4 -\) абсцисса вершины параболы, \(\displaystyle -\frac{b}{2a}=-4, \;\) \(b=8a.\)

Получим:

\(
\begin{cases}
-6a+8a=4, \\
b=8a;
\end{cases}
\)

\(
\begin{cases}
a=2, \\
b=16.
\end{cases}
\)

Подставив в уравнение \(4a-2b+c=3,\) получаем:

\(8-32+c=3; \)

\(c =27. \)

Значит, \(y=2x^2+16x+27.\)

Найдем точки пересечения графиков \(f(x)\) и \(g(x).\)

Для этих точек: \(f(x)=g(x)\)

\(3x^2+6x+3=2x^2+16x+27;\)

\(x^2-10x-24=0;\)

\(D=100+96=196; \; ~\sqrt{D}=14.\)

\(x=-2\) или \(x=12.\)

Абсцисса точки \(A\) равна \(-2\) (как и показано на рисунке). Тогда абсцисса точки \(B\) равна \(12\).

Ответ: 12.

Задача 5. На рисунке изображён график функции \(f(x)=\displaystyle \frac{kx+a}{x+b}.\) Найдите \(k\).

Решение:

На рисунке изображена гипербола. Ее график получен из графика функции \(y=\displaystyle \frac{k}{x}\) смещением на \(2\) единицы влево и на одну единицу вниз \(y=\displaystyle \frac{k}{x+2}-1.\)

Подробно об этом в теме: Преобразования графиков функций.

Чтобы найти \(k\), подставим координаты точки \((-1;-4)\) в формулу функции. На графике эта точка выделена жирным.

\(-4=\displaystyle \frac{k}{-1+2}-1; \; k=-3.\)

Формула функции: \(y=\displaystyle \frac{-3}{x+2}-1.\)

Чтобы проверить правильность решения, можно подставить в формулу функции координаты второй точки, которая выделена на графике, \((1;-2).\)

\(-2=\displaystyle \frac{-3}{1+2}-1,\) получили верное равенство.

Ответ: \(k=-3.\)

Задача 6. На рисунке изображены графики функций \(f(x)=-4x+9\) и \(g(x)=ax^2+bx+c, \) которые пересекаются в точках \(A\) и \(B\). Найдите ординату точки \(B\).

Решение:

На рисунке изображены прямая и парабола.

Найдем уравнение параболы. Обратим внимание на выделенные точки на графике:

\((-3;1)\) и \((-2;-1).\)

Также парабола пересекает ось ординат в точке \((0;1),\) значит, \(c=1.\)

Подставим значение с и координаты точек в формулу квадратичной функции и получим систему двух уравнений с двумя переменными:

\(
\begin{cases}
9a-3b+1=1, \\
4a-2b+1=-1;
\end{cases}\)

\(\begin{cases}
9a=3b, \\
4a-2b=-2;
\end{cases}
\)

\(
\begin{cases}
a=1, \\
b=3.
\end{cases}
\)

Формула квадратичной функции: \(g(x)=x^2+3x+1.\)

Найдем точки пересечения параболы и прямой. Для этого решим уравнение:

\(x^2+3x+1=-4x+9; \; x^2+7x-8=0.\)

Корни этого уравнения:

\(
\left[
\begin{gathered}
x=-8, \\
x=1.
\end{gathered}
\right.\)

Абсцисса точки \(B\) равна \(-8\). Найдем ее ординату:

\(y(-8)=-4\cdot(-8)+9=32+9=41. \)

Ответ: 41.

Задача 7. На рисунке изображены графики функций \(f(x)=\displaystyle \frac{k}{x}\) и \(g(x)=ax+b, \) которые пересекаются в точках \(A\) и \(B\). Найдите абсциссу точки \(B\).

Решение:

На рисунке изображены гипербола и прямая.

Найдем уравнение прямой:

Формула прямой: \(g(x)=ax+b.\)

На прямой выделены две точки: \(A(2;-1)\) и \(C(1;3).\)

Подставим по очереди их координаты в уравнение прямой и получим систему двух уравнений с двумя переменными:

\(
\begin{cases}
2a+b=-1, \\
a+b=3.
\end{cases}
\)

Вычтем из первого уравнения второе и получим \(a=-4; \; b=7.\)

\(g(x)=-4x+7\) – уравнение прямой.

Найдем уравнение гиперболы. Ее график симметричен относительно начала координат, значит, ее формула \(f(x)=\displaystyle \frac{k}{x}\).

Если \(x=1,\) то \(y=-2; \; k=y\cdot x=1\cdot(-2)=-2.\) Тогда уравнение гиперболы: \(f(x)=\displaystyle \frac{-2}{x}.\)

Найдем точки пересечения графиков функций. Для этого решим уравнение:

\(\displaystyle \frac{-2}{x}=-4x+7.\) Это дробно-рациональное уравнение.

Перенесем все в левую часть и приведем к общему знаменателю:

\(\displaystyle \frac{4x^2-7x-2}{x}=0; \;
\begin{cases}
4x^2-7x-2=0, \\
x\neq 0.
\end{cases}
\)

Решим квадратное уравнение:

\(4x^2-7x-2=0;\) его корни \(x=2\) и \(x=-\displaystyle \frac{1}{4}.\)

\(x=2\) - абсцисса точки \(A\), она показана на графике.

\(x=-\displaystyle \frac{1}{4}\) - абсцисса точки \(B\), которую нужно было найти.

Ответ: -0,25.

Задача 8. На рисунке изображены графики функции \(f(x)=a\sqrt{x}\) и \(g(x)=kx+b, \) которые пересекаются в точке \(A\). Найдите ординату точки \(A\).

Решение:

1) Найдем уравнение линейной функции. На ее графике выделены точки \((3;2)\) и \((6; 1).\)

Линейная функция на рисунке - убывающая, значит, \(k<0.\)

Формула линейной функции: \(y=\displaystyle -\frac{1}{3}x+b.\)

Чтобы найти \(b\), подставим координаты любой из выделенных точек. Возьмем, например, точку \((3; 2).\)

\(2=\displaystyle -\frac{1}{3}\cdot 3+b; \; b=3.\)

\(y=\displaystyle -\frac{1}{3}x+3\) - формула линейной функции.

2) Найдем коэффициент а в формуле второй функции \(f(x)=a\sqrt{x}\). На ее графике выделена точка \((4;-3).\)

Подставим координаты этой точки в уравнение:

\(-3=a\sqrt{4}; \; a=-1,5; \; f(x)=-1,5\sqrt{x}. \)

3) Найдем точки пересечения графиков функций. Для этого решим систему уравнений:

\(
\begin{cases}
y=\displaystyle -\frac{1}{3}x+3, \\
y=1,5\sqrt{x};
\end{cases}\)

\(-1,5\sqrt{x}=\displaystyle -\frac{1}{3}+3; \; 9\sqrt{x}=2x-18. \)

Решив это уравнение, найдем, что \(x = 36.\)

Это абсцисса точки пересечения графиков.

Найдем ординату этой точки: \( y(36)=-1,5\sqrt{36}=-1,5\cdot 6=-9. \)

Ответ: - 9.

Задача 9. На рисунке изображён график функции вида \(f(x) = kx+b + |cx - d|,\) где числа \(k, b, c\) и \(d\) — целые. Найдите \(d\) при условии, что \(d > 0. \)

Решение:

Расшифруем график.

Мы складываем график линейной функции \(y_1=kx+b\) и график модуля \(y_2=|cx-d|,\) который сдвинут вправо (так как \(d > 0\)) и сжат или растянут.

Мы складываем линейную и кусочно-линейную функции. При сложении графиков линейных функций угловой коэффициент суммы равен сумме угловых коэффициентов слагаемых.

\(x_0=2\) – точка излома графика \(f(x).\)

До точки \(x_0\) угловой коэффициент по модулю меньше, чем после точки \(x_0.\)

Значит, левее точки \(x_0\) коэффициент равен \(k_1=k-c,\) а правее точки \(x_0\) равен \(k_2=k+c\) и \(c>0. \)

Находим по графику, что \(k_1=-1, k_2=3.\) Получим систему:

\(
\begin{cases}
k-c=-1, \\
k+c=3.
\end{cases}
\)

Сложив уравнения системы, получим \(k=1.\)

Подставим \(k=1\) во второе уравнение системы, получим \(1+c=3,\) откуда \(c=2.\)

В точке излома графика \(x_0=2\) выполняется условие \(cx_0-d=0, \) тогда \(c\cdot2=d, \; 2c=d,\) а так как \(c=2,\) то \(d = 4.\)

Если \(x=0\), то \(f(0)=b+|d|=b+4\). По графику \(f(0)=5.\)

Получим уравнение \(b+4=5,\) откуда \(b=1.\)

Мы получили: \(k=1, \; b=1, \; c=2, \; d=4,\) значит, график на рисунке – это \(y=x+1+|2x-4|.\)

Ответ: 4.

Задача 10. На рисунке изображен график квадратичной функции \(y=f(x).\)
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.

1) \(f(x)>0\) при \(x>2.\)

2) Функция убывает на промежутке \([2;+\infty].\)

3) \(f(0)<f(5).\)