1. Авторская задача. Наполеон Бонапарт ростом был невысок – всего 5 футов и 2 дюйма, согласно историческим данным. Выразите рост Наполеона в сантиметрах, если 1 фут равен 0,305 м, а 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.
Посмотреть решение.
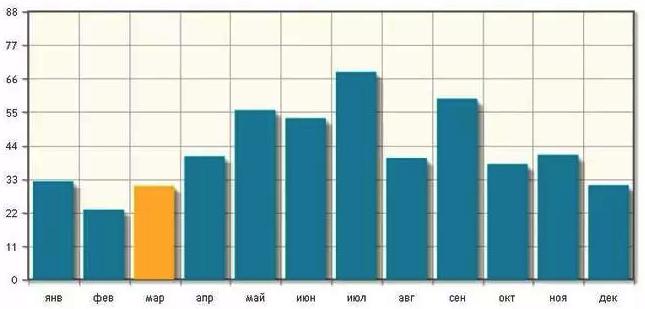
2. Авторская задача. На графике показано среднее количество осадков в Москве в течение года, в мм. Определите по рисунку, сколько месяцев из данного периода выпадало от 44 до 66 миллиметров осадков.
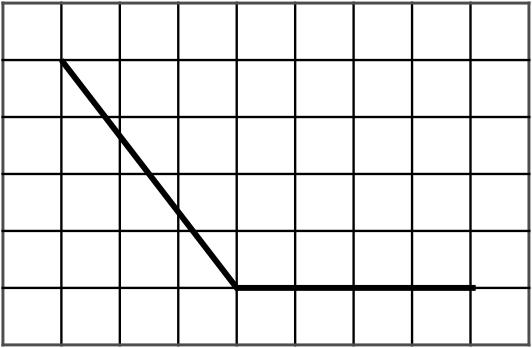
3. На клетчатой бумаге с размером клетки 1х1 изображен угол. Найдите косинус этого угла.
4. Авторская задача. Мини-пекарня продает пирожки с мясом, однако в среднем 2 пирожка из 10 оказываются без мяса. Покупатель купил 2 пирожка. Найдите вероятность того, что хотя бы в одном из них найдется мясо.
Посмотреть решение.
5. Найдите корень уравнения \(\displaystyle (\frac{1}{9})^{x-13}=3\)
Посмотреть решение.
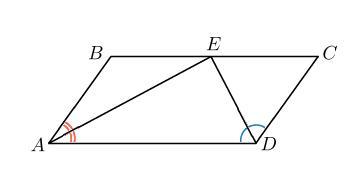
6. Авторская задача. Биссектрисы смежных углов параллелограмма АВСD пересекают сторону ВС в точке Е. Найдите угол АЕD. Ответ выразите в градусах.
7. Прямая \(y=-3x+8\) параллельна касательной к графику функции \(y-x^2+7x-6.\) Найдите абсциссу точки касания.
Посмотреть решение.
8. Авторская задача. Черепашка Грета живет в «ЕГЭ-Студии» с сентября прошлого года. За это время все линейные размеры Греты увеличились в 4 раза. Считая, что масса черепашки пропорциональна ее объему, определите, во сколько раз по сравнению с сентябрем прошлого года выросла масса Греты.
Посмотреть решение.
9. Найдите значение выражения \(\log_{a}(a^2b^3)\) , если \(\log_{a}b = 5\) и \(a = 7.\)
Посмотреть решение.
10. Уравнение процесса, в котором участвовал газ, записывается в виде \(\rho V^a=const \), где \(\rho\) (Па) – давление в газе, \(V\) – объём газа в кубических метрах, \(a\) – положительная константа. При каком наименьшем значении константы \(a\) уменьшение вдвое раз объёма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
Посмотреть решение.
11. Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
Посмотреть решение.
12. Найдите точку минимума функции \( y=(x+16)e^{x-16}\)
Посмотреть решение.
13. а) Решите уравнение \(2sin(\pi +x)\cdot sin(\frac{\pi }{2}+x)=sinx. \)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([3\pi ;\frac{9\pi }{2}]. \)
Посмотреть решение.
14. Боковые грани правильной четырехугольной пирамиды SABCD наклонены к плоскости основания под углом 45°.
а) Докажите, что апофема SM грани SCD перпендикулярна боковому ребру AS.
б) Найдите расстояние от вершины А до плоскости SDC, если АВ = 5.
Посмотреть решение.
15. Решите неравенство: \(\displaystyle \frac{8\cdot 7^x-4^{x\log_{2}7}-11}{(2x-1)^2}\geq 0.\)
Посмотреть решение.
16. Периметр прямоугольного треугольника АВС равен 72.
а) Докажите, что радиус R окружности, описанной вокруг треугольника АВС, равен его медиане, проведенной к гипотенузе АВ.
б) Найдите высоту СН, если она на 7 меньше, чем R.
Посмотреть решение.
17. Артем планирует в сентябре взять кредит на сумму 4 миллиона 100 тысяч рублей под 25 процентов годовых. Условия возврата кредита:
— каждый январь долг возрастает на 25 % по с равнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года), по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за 2 года)?
Посмотреть решение.
При каких значениях параметра a система имеет ровно 2 решения?
\(\left\{\begin{matrix}
(x^2+y^2-6y)(\sqrt{36-x^2}-y)=0\\
x=a(y+2)
\end{matrix}\right.\)
19. Назовем натуральное число хорошим, если в нем можно переставить цифры так, чтобы получившееся число делилось на 11.
а) Является ли число 1234 хорошим?
б) Является ли число 12345 хорошим?
в) Найти наибольшее хорошее число, состоящее из различных нечетных цифр.
Посмотреть решение.
Посмотреть ответы к задачам 1-12 Посмотреть видеоразбор
При разработке вариантов использованы условия задач с сайтов https://ege.sdamgia.ru/,
http://zadachi.mccme.ru, http://kvant.mccme.ru.