1. Авторская задача. Собираясь в отпуск в Таиланд, Яна меняет 55 тысяч рублей на доллары по курсу 63 рубля за доллар, чтобы по прилете в Бангкок поменять доллары на тайские баты по курсу 31,5 бата за доллар. Сколько тайских бат получит Яна?
Посмотреть решение.
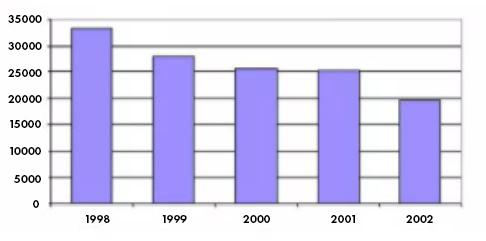
2. Авторская задача. На диаграмме показано изменение площади акватории Аральского моря в период с 1998 по 2002 год (в км²). В каком году из указанного периода площадь Аральского моря впервые стала меньше 25000 км²?
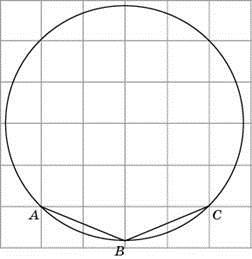
3. Найдите величину угла ABC. Ответ дайте в градусах.
4. Вероятность того, что клиент банка не вернет кредит, в период экономического роста равна 0,04, а в период экономического кризиса 0,2. Вероятность начала экономического кризиса оценивается в 0,45. Чему равна вероятность того, что клиент не вернет кредит?
Посмотреть решение.
5. Найдите корень уравнения \(\log_{5}(5-x)=2\log_{5}3.\)
Посмотреть решение.
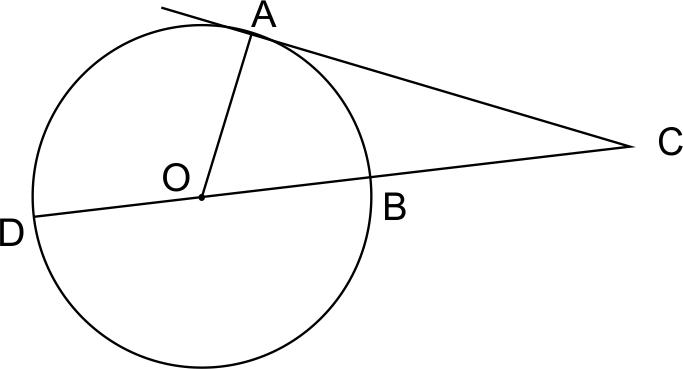
6. Угол ACO равен 24°. Его сторона CA касается окружности. Найдите градусную величину большей дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.
7. Прямая \(y=5x+5\) является касательной к графику функции \(f(x)=8x^2+29x+c.\) Найдите c.
Посмотреть решение.
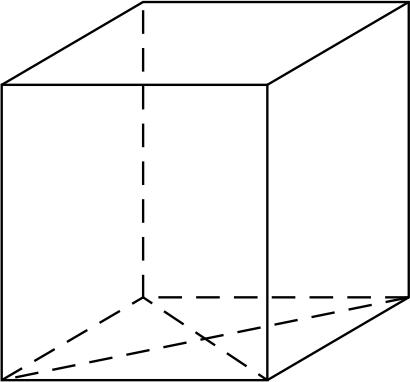
8. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
9. Найдите значение выражения \(\displaystyle \frac{15\sqrt[5]{\sqrt[28]{a}}-7\sqrt[7]{\sqrt[20]{a}}}{2\sqrt[35]{\sqrt[4]{a}}}\) при \(a> 0.\)
Посмотреть решение.
10. Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле \(A(\omega )=\displaystyle \frac{A_0\omega ^2_p}{\begin{vmatrix}
\omega ^2_p-\omega ^2
\end{vmatrix}},\) где \(\omega \) – частота вынуждающей силы (в \(c^{-1}\)), \(A_0\) – постоянный параметр, \(\omega _p=360c^{-1} \) – резонансная частота. Найдите максимальную частоту \(\omega \), меньшую резонансной, для которой амплитуда колебаний превосходит величину \(A_0\) не более чем на 12,5% Ответ выразите в \(c^{-1}\).
Посмотреть решение.
11. Весной катер идёт против течения реки в \(1\frac{2}{3}\) раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в \(1\frac{1}{2}\) раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Посмотреть решение.
12. Найдите точку максимума функции \(y=\log_{2}(2+2x-x^2)-2.\)
Посмотреть решение.
13. Дано уравнение
\(log_{cos x} ( cos 2x - sin x ) = 0\)
а) решите уравнение
б) найдите все корни, принадлежащие отрезку [ -3π; 2π].
Посмотреть решение.
14. В основании призмы \(ABCA_1B_1C_1\) лежит правильный треугольник, вершина \(C_1\) проецируется в центр Q основания АВС.
а) Докажите, что плоскости \(ABC_1\) и \(QCC_1 \) перпендикулярны,
б) Найдите угол между прямой \(AA_1\) и плоскостью \(ABC_1\), если боковое ребро призмы равно стороне основания.
Посмотреть решение.
15. Решите неравенство: \(\displaystyle \frac{\log_{x-2}(3x-1)+\log_{x-2}\frac{1}{x}}{x-4}\leq 0.\)
Посмотреть решение.
16. Четырехугольник КLMN можно вписать в окружность, причем LM = MN, отрезки КМ и LN пересекаются в точке Р.
а) докажите, что \(KM \cdot MP = LM^2\)
б) Известно, что КМ = 8, угол LMN равен 150 градусов. Найдите площадь четырехугольника КLMN.
Посмотреть решение.
17. 15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Посмотреть решение.
18. Найти все значения параметра а, при каждом из которых уравнение
\(sin(x-3a)+sin(\displaystyle\frac{x^2-6x+7a}{2})=4x-x^2-a\)
не имеет действительных решений.
Посмотреть решение.
19. На доске написано 30 различных натуральных чисел, каждое из которых либо четное, либо его десятичная запись заканчивается на цифру 7. Сумма написанных чисел равна 810.
а) Может ли быть 24 четных числа?
б) Может ли быть на доске ровно два числа, оканчивающихся на 7?
в) Какое наименьшее количество чисел с последней цифрой 7 может быть на доске?
Посмотреть решение.
Посмотреть ответы к задачам 1-12 Посмотреть видеоразбор
При разработке вариантов использованы условия задач с сайтов https://ege.sdamgia.ru/,
http://zadachi.mccme.ru, http://kvant.mccme.ru.






























