1. Авторская задача. В среднем учащиеся «ЕГЭ-Студии» съедают за учебный день 1,8 кг шоколадных конфет, при условии, что на занятия не пришел Гриша. Если Гриша приходит на занятия, то он съедает 0,5 кг конфет. На сколько дней хватит 10 кг шоколадных конфет, если Гриша собирается посетить «ЕГЭ-Студию» ровно 2 раза?
Посмотреть решение.
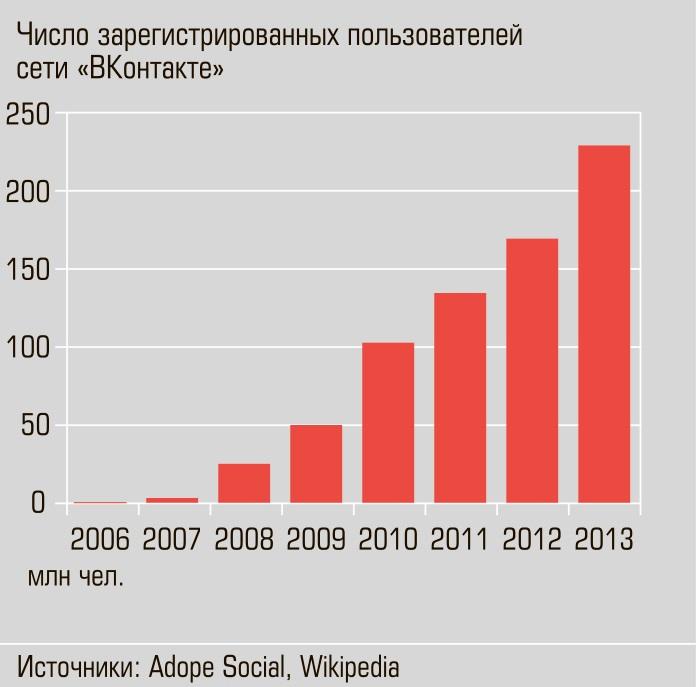
2. Авторская задача. На диаграмме показан рост числа пользователей сети «ВКонтакте» в период с 2006 по 2013 год (в млн. человек). Определите, во сколько раз выросло число пользователей в 2010 году по сравнению с 2009 годом. Если необходимо, округлите ответ до целых.
3. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
4. Авторская задача. Склад оборудован двумя датчиками сигнализации различной конструкции, которые подают звуковой сигнал, если в помещение проникает посторонний. Вероятность выхода из строя в течение года для первого датчика равна 0,1 и для второго 0,2. Найдите вероятность того, что в течение года хотя бы один датчик сигнализации останется исправным.
Посмотреть решение.
5. Найдите корень уравнения \(3^{\log_{9}(5x-5)}=5.\)
Посмотреть решение.
6. Радиус окружности, описанной вокруг правильного треугольника АВС, равен \(2\sqrt{3}\). Найдите сторону АВ.
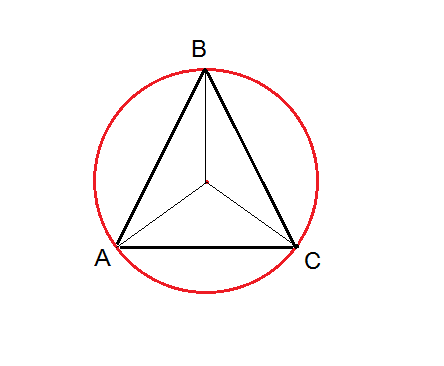
7. На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите количество точек минимума функции f(x) на этом интервале.
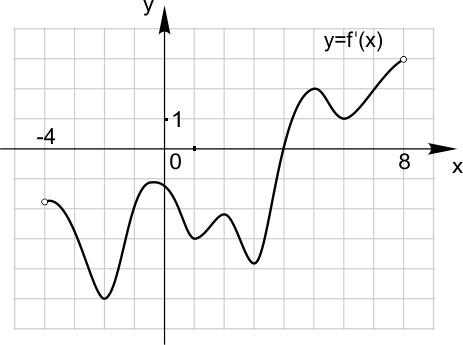
8. Авторская задача. Стеклянный шар помещен в цилиндрическую банку с крышкой так, что он касается ее стенок, дна и крышки. Во сколько раз объем банки больше объема шара?
Посмотреть решение.
9. Найдите значение выражения \(\displaystyle \frac{24(sin^217^{\circ}-cos^217^{\circ})}{cos34^{\circ}}
\)
Посмотреть решение.
10. Мотоциклист, движущийся по городу со скоростью \(v_0=57\) км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением \(a=12\) км/ч². Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением \(S=v_0t+\frac{at^2}{2}. \) Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
Посмотреть решение.
11. Теплоход проходит по течению реки до пункта назначения 255 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 1 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход возвращается через 34 часа после отплытия из него. Ответ дайте в км/ч.
Посмотреть решение.
12. Найдите наибольшее значение функции \(y=14x-7tgx-3,5\pi +11 \) на отрезке \( [-\displaystyle \frac{\pi }{3}; \displaystyle \frac{\pi }{3}].\)
Посмотреть решение.
13. а) Решите уравнение \( 9^{sinx}+9^{-sinx}=\displaystyle\frac{10}{3}.\)
б) Укажите корни этого уравнения, принадлежащие отрезку \( [-\displaystyle\frac{7\pi }{2};-2\pi].\)
Посмотреть решение.
14. В основании прямой треугольной призмы \(ABCA_1B_1C_1\) лежит прямоугольный треугольник ABC с прямым углом C, AC = 4, BC = 16, \(AA_1=4\sqrt{2}.\) Точка Q — середина ребра \(A_1B_1\), а точка P делит ребро \(B_1C_1\) в отношении 1 : 2, считая от вершины \(C_1\). Плоскость APQ пересекает ребро \(CC_1\) в точке M.
а) Докажите, что точка M является серединой ребра \(CC_1\).
б) Найдите расстояние от точки \(A_1\) до плоскости APQ.
Посмотреть решение.
15. Решите неравенство: \((3^{x+2}+3^{2-x})x^2\geq \displaystyle\frac{45x^2}{2}. \)
Посмотреть решение.
16. Угол между касательными РВ и РС, проведенными из точки Р к окружности S, равен 60°. Отрезок, соединяющий центр окружности S с точкой Р, пересекается с окружностью S в точке Т, а с отрезком ВС – в точке М. Прямая ВТ пересекает отрезок РС в точке Е.
а) Докажите, что точки Р, В, М и Е лежат на одной окружности.
б) Найдите радиус окружности, описанной вокруг четырехугольника РВМЕ, если радиус окружности S равен четырем.
Посмотреть решение.
17. Максим открыл вклад на сумму 312500 рублей под 20% годовых и каждый год после начисления процентов добавлял ко вкладу одну и ту же сумму Х. Известно, что через 4 года после начисления процентов и внесения дополнительной суммы Х вклад стал равен 983500 рублей. Какую сумму Максим ежегодно добавлял ко вкладу?
Посмотреть решение.
18. Найти все значения параметра \(a\), при каждом из которых среди значений функции \(y=\displaystyle \frac{x^2-2x+a}{6+x^2}\) есть ровно одно целое число.
Посмотреть решение.
19. По окружности расставляют 48 ненулевых целых чисел с общей суммой 20. При этом любые два стоящих рядом числа должны отличаться не более чем на 7 и среди любых четырёх подряд идущих чисел должно быть хотя бы одно положительное.
а) Среди таких 48 чисел найдите наибольшее возможное количество положительных.
б) Среди таких 48 чисел найдите наименьшее возможное количество положительных.
Посмотреть решение.
Посмотреть ответы к задачам 1-12 Посмотреть видеоразбор
При разработке вариантов использованы условия задач с сайтов https://ege.sdamgia.ru/,
http://zadachi.mccme.ru, http://kvant.mccme.ru.






























