В этом варианте - только задачи из Банка заданий ФИПИ. Сложность варианта соответствует сложности реальных задач ЕГЭ.
1. Бегун пробежал 50 м за 5 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
Посмотреть решение.
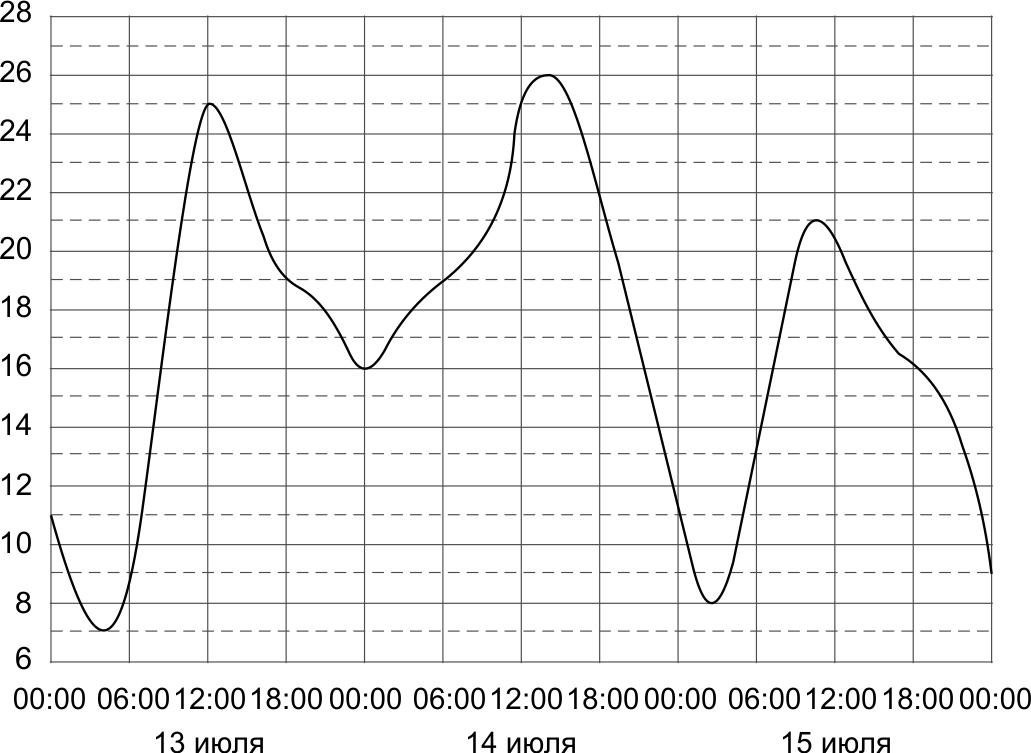
2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 15 июля. Ответ дайте в градусах Цельсия.
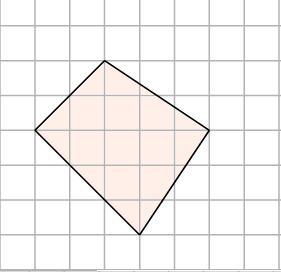
3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см×1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
4. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
Посмотреть решение.
5. Найдите корень уравнения \(\sqrt{\displaystyle \frac{6}{4x-54}}=\displaystyle \frac{1}{7}.\)
Посмотреть решение.
6. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
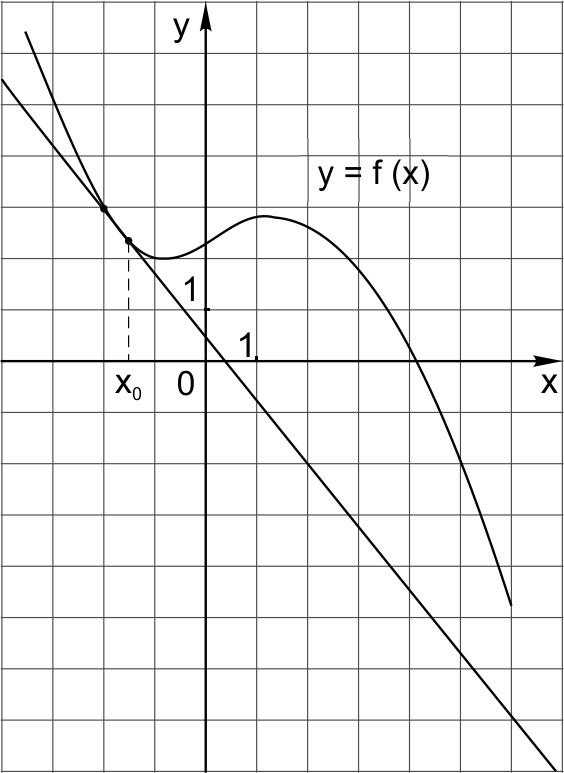
7. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции f(x) в точке \(x_0\).
8. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен \(28\sqrt{2}.\) Найдите образующую конуса.
Посмотреть решение.
9. Найдите значение выражения \((\displaystyle \frac{2^{\frac{1}{3}}\cdot 2^{\frac{1}{4}}}{\displaystyle \sqrt[12]{2}})^2.\)
Посмотреть решение.
10. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в Кельвинах) от времени работы: \(T(t)=T_0+bt+at^2\), где t – время в минутах, \(T_0=1400K,~ a=-10\) к / мин² , b=200 К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
Посмотреть решение.
11. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Посмотреть решение.
12. Найдите наименьшее значение функции \(y=2^{x^2+2x+5}\)
Посмотреть решение.
13. а) Решите уравнение \(\displaystyle \frac{1}{sin^2x}-\displaystyle \frac{3}{sinx}+2=0.\)
б) Укажите корни этого уравнения, принадлежащие отрезку \([-\displaystyle \frac{5\pi }{2};-\pi].\)
Посмотреть решение.
14. На ребре \(AA_1\) прямоугольного параллелепипеда \(ABCDA_1B_1C_1D_1\) взята точка Е, так что
\( A_1E :EA=6:1\), на ребре \(BB_1\) — точка F так, что \(B_1F:FB=3:4\), точка Т — середина ребра \(B_1C_1\). Известно, что \( AB=4\sqrt{2} \) , \(AD=30, \) \(AA_1=35 \).
а) Докажите, что плоскость EFT проходит через вершину \(D_1\) .
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
Посмотреть решение.
15. Решите неравенство \(\displaystyle \log_{5-x}\frac{x+2}{(x-5)^4}\geq -4\)
Посмотреть решение.
16. В треугольнике АВС угол ВАС равен 60 градусов, угол АВС равен 45 градусов. Продолжения высот треугольника АВС пересекают описанную вокруг него окружность в точках М, Т, Р.
а) Докажите, что треугольник МТР прямоугольный.
б) Найдите площадь треугольника МТР, если ВС = 12.
Посмотреть решение.
17. 15 января планируется взять кредит в банке на сумму 0,3 млн рублей на 24 месяца. Условия его возврата таковы: 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца, со 2-го по 14-е число каждого месяца необходимо выплатить часть долга, 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму нужно вернуть банку в течение второго года кредитования?
Посмотреть решение.
18. Найдите все значения \(a,\) при каждом из которых функция \(f(x)=\begin{vmatrix}
\begin{vmatrix}
x \end{vmatrix} -2
\end{vmatrix}-ax+8a\) принимает значение, равное 2, в двух различных точках.
Посмотреть решение.
19. Петя умножил некоторое натуральное число на соседнее натуральное число и получил произведение, равное а. Вася умножил некоторое четное натуральное число на соседнее четное натуральное число и получил произведение, равное b.
а) Может ли модуль разности чисел a и b равняться 8?
б) Может ли модуль разности чисел a и b равняться 11?
в) Какие значения может принимать модуль разности чисел a и b?
Посмотреть решение.
Посмотреть ответы к задачам 1-12 Посмотреть видеоразбор
При разработке вариантов использованы условия задач с сайтов https://ege.sdamgia.ru/,
http://zadachi.mccme.ru, http://kvant.mccme.ru.






























