В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №11 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.
Как формулируется задание 11 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.
Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.
Вот необходимая теория для решения задания №11 ЕГЭ.
5 типов элементарных функций и их графики
Преобразование графиков функций
Да, теоретического материала здесь много. Но он необходим — и для решения задания 11 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.
Рекомендации:
Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)
Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?
Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.
Задание 11 в формате ЕГЭ-2021
Линейная функция
1. На рисунке изображён график функции \(f\left(x\right)=kx+b\). Найдите значение \(x\), при котором \(f\left(x\right)=-13,5.\)
Решение:
Найдем, чему равны \(k\) и \(b.\) График функции проходит через точки \((3; 4)\) и \((-1; -3).\)
Подставив по очереди координаты этих точек в уравнение прямой \(y = kx + b,\) получим систему:
\(\left\{ \begin{array}{c}
3k+b=4 ,\\
-k+b=-3. \end{array}
\right.\)
Вычтем из первого уравнения второе:
\(\left\{ \begin{array}{c}
4k=7, \\
-k+b=-3 ;\end{array}
\right. \left\{ \begin{array}{c}
k=\displaystyle \frac{7}{4} ,\\
b=\displaystyle -\frac{5}{4}. \end{array}
\right. \)
Уравнение прямой имеет вид:
\(\displaystyle y=\frac{7}{4}x-\frac{5}{4}.\)
Найдем, при каком \(x\) значение функции равно -13,5.
\(\displaystyle \frac{7}{4}x-\frac{5}{4}=-13,5;\)
\(7x-5=-54;\)
\(7x=-49;\)
\(x=-7.\)
Ответ: -7.
2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Решение:
Запишем формулы функций.
Одна из них проходит через точку \((0; 1)\) и ее угловой коэффициент равен -1. Это линейная функция \(y=-x+1.\)
Другая проходит через точки \((-1; -1)\) и \((-2; 4)\).
Подставим по очереди координаты этих точек в формулу линейной функции \(y=kx+b.\)
\(\left\{ \begin{array}{c}
-k+b=-1, \\
-2k+b=4. \end{array}
\right. \)
Вычтем из первого уравнения второе.
\(k=-5;\) тогда \(b=-6.\)
Прямая задается формулой: \(y=-5x-6.\)
Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:
\(\left\{ \begin{array}{c}
y=-x+1, \\
y=-5x-6; \end{array}
\right.\left\{ \begin{array}{c}
-x+1=-5x-6,\\
x=-\displaystyle \frac{7}{4}=-1,75. \end{array}\right.\)
Ответ: -1,75.
3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Решение:
Прямая, расположенная на рисунке ниже, задается формулой \(y=x+1,\) так как ее угловой коэффициент равен 1 и она проходит через точку \((-3; -2).\)
Для прямой, расположенной выше, угловой коэффициент равен \(\displaystyle \frac{3}{2}=1,5.\)
Эта прямая проходит через точку \((-2; 4)\), поэтому: \(1,5\cdot \left(-2\right)+b=4; \ b=7,\) эта прямая задается формулой \(y=1,5x+7.\)
Для точки пересечения прямых:
\(x+1=1,5x+7;\)
\(0,5x=-6;\)
\(x=-12.\)
Ответ: -12.
Квадратичная функция. Необходимая теория
4. На рисунке изображен график функции \(y=ax^2+bx+c.\) Найдите \(b.\)
Решение:
На рисунке — квадратичная парабола \(y={\left(x-a\right)}^2,\) полученная из графика функции \(y=x^2\) сдвигом на 1 вправо, то есть \(a=1.\)
Получим: \(f\left(x\right)={\left(x-1\right)}^2=x^2-2x+1;\)
\(b=-2.\)
Ответ: -2.
5. На рисунке изображен график функции \(y={\left(x-c\right)}^2\). Найдите \(c.\)
Решение:
На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при \(x^2\) положительный. График сдвинут относительно графика функции \(y=x^2\) на 1 единицу вправо вдоль оси \(Ox.\)
Формула функции имеет вид \(y={\left(x-1\right)}^2.\)
Значит, \(c = 1.\)
Ответ: 1
6. На рисунке изображён график функции \(f\left(x\right)=2x^2+bx+c.\) Найдите \(f\left(-5\right).\)
Решение:
График функции \(y=2x^2+bx+c\) проходит через точки с координатами \((1; 1)\) и \((-2; -2).\) Подставляя координаты этих точек в формулу функции, получим:
\(\left\{ \begin{array}{c}
2+b+c=1,\\
2\cdot 4-2b+c=-2; \end{array}
\right. \)
\(\left\{ \begin{array}{c}
b+c=-1, \\
-2b+c=-10; \end{array}
\right. \; \) отсюда \(b=3, \ c=-4.\)
Формула функции имеет вид:
\(f\left(x\right)=2x^2+3x-4;\)
\(f\left(-5\right)=2\cdot 25-3\cdot 5-4=31.\)
Ответ: 31.
7. На рисунке изображены графики функций \(f\left(x\right)=5x+9\) и \(g\left(x\right)=ax^2+bx+c,\) которые пересекаются в точках \(A\) и \(B.\) Найдите абсциссу точки \(B.\)
Решение:
Найдем \(a, \ b\) и \(c\) в формуле функции \(g\left(x\right)=ax^2+bx+c\). График этой функции пересекает ось ординат в точке (0; -3), поэтому \(c=-3.\)
График функции \(g(x)\) проходит через точки \((-1; -3)\) и \((2; 3).\) Подставим по очереди координаты этих точек в формулу функции:
\(\left\{ \begin{array}{c}
a-b-3=-3, \\
4a+2b-3=3; \end{array}
\right. \; \) отсюда \(a=b=1;\)
\(g\left(x\right)=x^2+x-3;\)
Найдем абсциссу точки \(B.\) Для точек \(A\) и \(B: \ f\left(x\right)=g(x).\)
\(5x+9=x^2+x-3;\)
\(x^2-4x-12=0.\)
\(x=-2\) (это абсцисса точки \(A\)) или \(x=6\) (это абсцисса точки \(B\)).
Ответ: 6.
Степенные функции. Необходимая теория
8. На рисунке изображены графики функций \(\displaystyle f\left(x\right)=\frac{k}{x}\) и \(g\left(x\right)=ax+b\), которые пересекаются в точках \(A\) и \(B.\) Найдите абсциссу точки \(B.\)
Решение:
График функции \(\displaystyle y=\frac{k}{x}\) проходит через точку \((2; 1);\) значит, \(\displaystyle \frac{k}{2}=1;\)
\(\displaystyle k=2,\ \; f\left(x\right)=\frac{2}{x}.\)
График функции \(g\left(x\right)=ax+b\) проходит через точки \((2; 1)\) и \((1; -4), \ a=5\) — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси \(X\)); тогда \(5\cdot 2+b=1; \ b=-9.\)
Для точек \(A\) и \(B\) имеем: \(f\left(x\right)=g\left(x\right);\)
\(\displaystyle \frac{2}{x}=5x-9;\)
\(5x^2-9x-2=0.\)
Отсюда \(x=2\) (абсцисса точки \(A\)) или \(x=-0,2\) (абсцисса точки \(B\)).
Ответ: -0,2.
9. На рисунке изображён график функции \(f\left(x\right)=k\sqrt{x}\). Найдите \(f (6,76).\)
Решение:
Функция задана формулой: \(y=k\sqrt{x}.\)
Ее график проходит через точку \((4; 5);\) значит, \(k\cdot \sqrt{4}=5; \ k=2,5; \ f\left(x\right)=2,5\sqrt{x}.\)
Тогда \(f\left(6,76\right)=2,5\cdot \sqrt{6,76}=2,5\cdot 2,6=6,5.\)
Ответ: 6,5.
10. На рисунке изображен график функции \(f\left(x\right)=\sqrt{ax}\). Найдите \(f\left(-25\right)\).
Решение:
График функции на рисунке симметричен графику функции \(y=\sqrt{x}\) относительно оси \(Y\). Он проходит через точку \((-1; 1).\)
Значит, формула изображенной на рисунке функции: \(y=\sqrt{-x}, \ a = - 1.\) Тогда \(f\left(-25\right)=\sqrt{25} = 5.\)
Ответ: 5.
Показательная функция. Необходимая теория
11. На рисунке изображён график функции \(f\left(x\right)=a^{x+b}.\) Найдите \(f\left(-7\right).\)
Решение:
График функции проходит через точки \((-3; 1)\) и \( (1; 4)\). Подставив по очереди координаты этих точек в формулу функции \(f\left(x\right)=a^{x+b},\) получим:
\(\left\{ \begin{array}{c}
a^{-3+b}=1, \\
a^{1+b}=4. \end{array}
\right.\)
Поделим второе уравнение на первое:
\(a^{1+b+3-b}=4; \; a^4=4;\; a=\sqrt{2}.\)
Подставим во второе уравнение:
\(\displaystyle {\sqrt{2}}^{1+b}=4; \; 2^{\frac{1+b}{2}}=2^2; \; 1+b=4;\; b=3.\)
\(\displaystyle f\left(x\right)={\left(\sqrt{2}\right)}^{x+3}; \; f\left(-7\right)={\left(\sqrt{2}\right)}^{-7+3}={\left(\sqrt{2}\right)}^{-4}=\frac{1}{4}=0,25.\)
Ответ: 0,25.
12. На рисунке изображен график функции \(y=a\cdot 4^x.\) Найдите \(a.\)
Решение:
График функции \(y=a\cdot 4^x\) проходит через точку \(\left(0;2\right).\) Это значит, что \(y\left(0\right)=2;\)
\(a\cdot 4^0=2; \ a=2,\) формула функции имеет вид: \(y=2\cdot 4^x.\)
Ответ: 2.
Логарифмическая функция. Необходимая теория
13. На рисунке изображён график функции \(f\left(x\right)={{log}_a \left(x+b\right)}.\) Найдите \(f\left(11\right).\)
Решение:
График функции \(y={{log}_a \left(x+b\right)\ }\) проходит через точки \((-3; 1)\) и \((-1; 2)\). Подставим по очереди эти точки в формулу функции.
\(\left\{ \begin{array}{c}
{{log}_a \left(-3+b\right)=1 }, \\
{{log}_a \left(-1+b\right) }=2. \end{array}
\right.\)
Отсюда: \(\left\{ \begin{array}{c}
b-3=a, \\
b-1=a^2. \end{array} \right.\)
Вычтем из второго уравнения первое:
\(a^2-a=2; \ a^2-a-2=0;\)
\(a=2\) или \(a=-1\) — не подходит, так как \(a > 0\) (как основание логарифма).
Тогда \(b=a+3=5; \ f\left(x\right)={{log}_2 \left(x+5\right)}; \ f\left(11\right)={{log}_2 16=4.}\)
Ответ: 4.
14. На рисунке изображен график функции \(f\left(x\right)=a{{log}_5 x }-c\). Найдите \(f(0,2).\)
Решение:
График логарифмической функции на рисунке проходит через точки \(\left(1;-2\right)\) и \(\left(5;3\right)\). Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:
\(\left\{ \begin{array}{c}
a{{log}_5 1\ }-c=-2, \\
a{{log}_5 5\ }-c=3; \end{array}
\right.\)
\(\left\{ \begin{array}{c}
-c=-2 ,\\
a-c=3; \end{array}
\right.\)
\(\left\{ \begin{array}{c}
c=2, \\
a=5. \end{array}
\right.\)
Формула функции: \(f\left(x\right)=5{{log}_5 x }-2.\)
Найдем \(\displaystyle f\left(0,2\right)=f\left(\frac{1}{5}\right):\)
\(\displaystyle 5\cdot {{log}_5 \frac{1}{5}\ }-2=-5-2=-7.\)
Ответ: -7.
Тригонометрические функции. Необходимая теория
15. На рисунке изображён график функции \(f\left(x\right)=a{sin x}+b.\) Найдите \(b.\)
Решение:
График функции \(y=a{sin x+b }\) сдвинут на 1,5 вверх; \(f\left(0\right)=1,5.\) Значит, \(b=1,5.\) Амплитуда \(a=2\) (наибольшее отклонение от среднего значения).
Это график функции \(f\left(x\right)=2{sin x}+1,5.\) Он получен из графика функции \(y={sin x}\) растяжением в 2 раза по вертикали и сдвигом вверх на \(1,5.\)
Ответ: \(b=1,5.\)
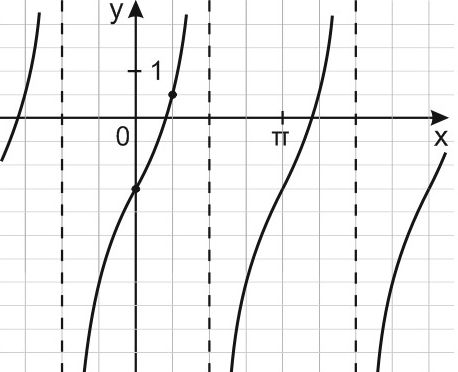
16. На рисунке изображён график функции \(f\left(x\right)=a\ tgx+b.\) Найдите \(a.\)
Решение:
На рисунке — график функции \(f\left(x\right)=a\ tgx+b.\) Так как \(f\left(0\right)=-1,5, \ b=-1,5.\)
График функции проходит через точку \(A \displaystyle \left(\frac{\pi}{4}; \; \frac{1}{2}\right).\)
Подставим \(b = - 1,5\) и координаты точки \(A\) в формулу функции.
\(\displaystyle a \ tg \frac{\pi}{4}-1,5=\frac{1}{2}.\)
Так как \(\displaystyle tg \frac{\pi}{4}=1,\) получим: \(a = 2.\)
Ответ: 2.
17. На рисунке изображен график периодической функции \(y = f(x).\) Найдите значение выражения \(f (21)- f (-9).\)
Решение:
Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если \(y\left(1\right)=2,5,\) то \(y\left(-1\right)=-2,5.\)
Пользуясь периодичностью функции \(f\left(x\right) \), период которой \(T = 4\), получим:
\(f\left(21\right)=f\left(1+4\cdot 5\right)=f\left(1\right)=2,5;\)
\(f\left(-9\right)=f\left(-1-4\cdot 2\right)=f\left(-1\right)=-2,5;\)
\(f\left(21\right)-f\left(-9\right)=2,5-\left(-2,5\right)=5.\)
Ответ: 5.
Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.