1. Авторская задача. Заработная плата Николая составляет 120 тысяч рублей в месяц, а заработная плата Андрея 144 тысячи рублей в месяц. На сколько процентов зарплата Андрея больше зарплаты Николая?
Посмотреть решение.
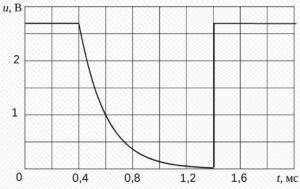
2. Авторская задача. На графике показано изменение напряжения на конденсаторе в зависимости от времени. Определите, за какое время напряжение на конденсаторе уменьшилось от 1 В до нуля. Ответ выразите в мс.
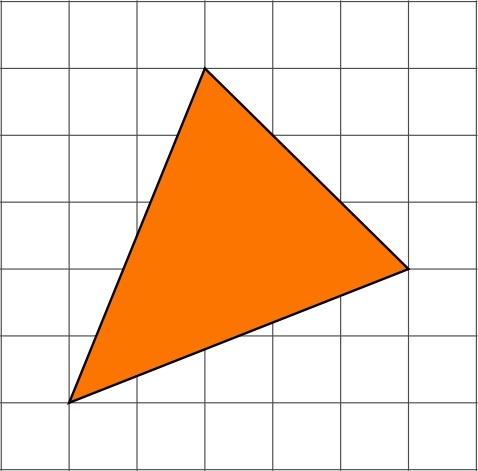
3. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см.
4. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Посмотреть решение.
5. Найдите корень уравнения: \(\sqrt{-72-17x}=-x\). Если уравнение имеет более одного корня, укажите меньший из них.
Посмотреть решение.
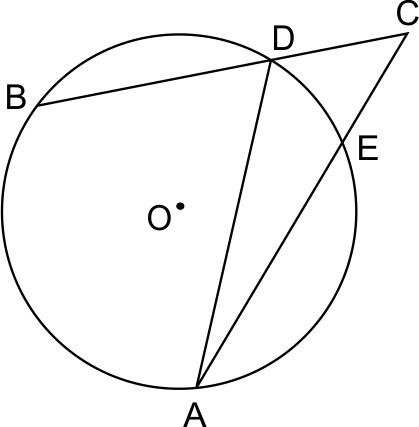
6. Угол ACB равен \(14,5^{\circ}.\) Градусная величина дуги AB окружности, не содержащей точек D и E, равна \(117^{\circ}\). Найдите угол DAE. Ответ дайте в градусах.
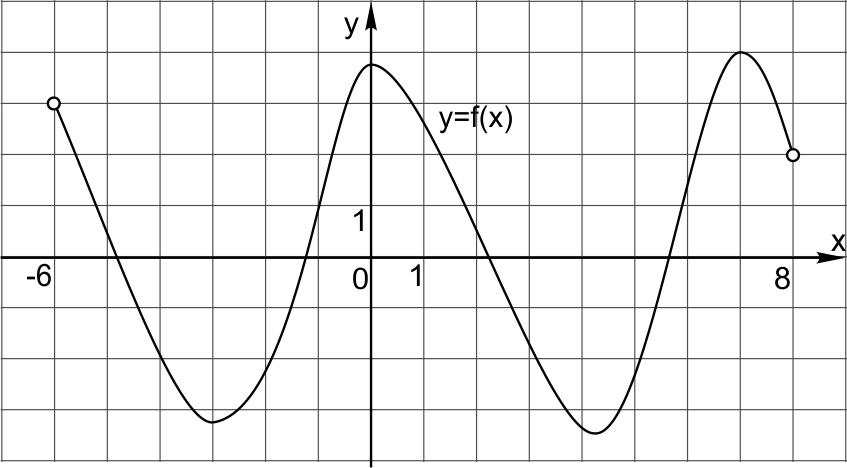
7. На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
8. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.
Посмотреть решение.
9. Найдите значение выражения \(\displaystyle \frac{\sqrt[15]{5}\cdot 5\sqrt[10]{5}}{\sqrt[6]{5}}. \)
Посмотреть решение.
10. Перед отправкой тепловоз издал гудок с частотой \(f_0=440\) Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка \(f\) больше первого: она зависит от скорости тепловоза по закону \(f(v)=\displaystyle \frac{f_0}{1-\frac{v}{c}}\) (Гц), где c – скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а \(c=315\) м/с. Ответ выразите в м/с.
Посмотреть решение.
11. Клиент А сделал вклад в банке в размере 7700 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал клиент Б. Еще ровно через год клиенты А и Б закрыли вклады и забрали все накопившиеся деньги. При этом клиент А получил на 847 рублей больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
Посмотреть решение.
12. Найдите наибольшее значение функции \(y=x^3-6,5x^2+14x-14\) на отрезке [-4; 3].
Посмотреть решение.
13. а) Решите уравнение \(4sin^2=tgx\)
б) Укажите корни этого уравнения, принадлежащего отрезку \([-\pi ;0] \)
Посмотреть решение.
14. Точки М и N – середины ребер соответственно АВ и СD треугольной пирамиды АВСD, О – точка пересечения медиан грани АВС.
а) Докажите, что прямая DO проходит через середину отрезка MN.
б) Найдите угол между прямыми MN и ВС, если АВСD – правильный тетраэдр.
Посмотреть решение.
15. Решите неравенство \( \log_{2}^2(3x-1)+\log_{3x-1}^22-\log_{2}(3x-1)^2-\log_{3x-1}4+2\leq 0 ;\)
Посмотреть решение.
16. Боковые стороны АВ и CD трапеции ABCD являются диаметрами окружностей, пересекающихся в точках М и N.
а) Докажите, что МN и АD перпендикулярны.
б) Найдите MN, если боковые стороны трапеции равны 12 и 16, а сумма проекций диагоналей на большее основание равна 20.
Посмотреть решение.
17. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— Каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 77 760 руб, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 131 760 руб, то кредит будет полностью погашен за 2 года. Найдите r.
Посмотреть решение.
18. Найдите все значения параметра \(a\), при каждом из которых уравнение
\((1+sinx)^4-4sinx=7-a-a^2\) не имеет решений.
Посмотреть решение.
19. Про три различных натуральных числа известно, что они являются длинами сторон некоторого тупоугольного треугольника.
а) Может ли отношение большего из этих чисел к меньшему из них быть равно \(\displaystyle \frac{13}{7}\)?
б) Может ли отношение большего из этих чисел к меньшему из них быть равно \(\displaystyle \frac{8}{7}\)?
Посмотреть решение.
Посмотреть ответы к задачам 1-12 Посмотреть видеоразбор
При разработке вариантов использованы условия задач с сайтов https://ege.sdamgia.ru/,
http://zadachi.mccme.ru, http://kvant.mccme.ru.






























