Часть 1. Задания с кратким ответом
1. Анна Малкова
Девочка Маша уехала учиться в Лондон и через 3 года написала бабушке, что выросла на 1 фут и 3 дюйма. У бабушки нет ни ноутбука, ни калькулятора. Помогите посчитать, на сколько сантиметров выросла внучка! 1 фут равен 12 дюймам, 1 дюйм считаем равным 2,54 см. Ответ округлите до целого числа сантиметров.
Посмотреть ответ Посмотреть решение
2. Наталья Гаврилова
На рисунке показано количество книг, выпущенных в России с 2003 г. по 2017 г. По горизонтали указан год, по вертикали – количество книг в млн. Определите по рисунку среднее количество книг в год (в миллионах экземпляров), выпущенных в России с 2010 г. по 2015 г. включительно.
Посмотреть ответ Посмотреть решение
3. Точка В – общий центр двух концентрических окружностей, большая из которых проходит через начало координат. По данным рисунка найдите ординату точки В.
Посмотреть ответ Посмотреть решение
4. Анна Малкова
Узнав о появлении компьютерного вируса Angry worm* , пользователь Фил защитил свой ноутбук новой антивирусной программой, которая приостанавливает работу компьютера при подозрении на вирус.
Известно, что в случае наличия вируса Angry worm на компьютере программа распознает его с вероятностью 0,9.
Если компьютер не заражен этим вирусом, программа может дать сигнал ложной тревоги с вероятностью 0,02.
Известно также, что в день, когда Фил запускает антивирус на своем ноутбуке, 4% всех компьютеров в мире заражены вирусом Angry worm.
С какой вероятностью работа ноутбука Фила будет приостановлена в день запуска антивирусной программы?
* Название вымышленное, возможные совпадения случайны.
Посмотреть ответ Посмотреть решение
5. Наталья Гаврилова
Решите уравнение \(\displaystyle log_{0,4} (x-5)=log_{0,4} (tg \frac{\pi}{4}).\)
Посмотреть ответ Посмотреть решение
6. Анна Малкова
Точка Е – середина стороны АС, а М – точка пересечения медиан треугольника АВС. Площадь треугольника АЕМ равна 1,5. Найдите площадь треугольника АВС.
Посмотреть ответ Посмотреть решение
7. На рисунке изображён график функции \(y=f(x).\) На оси абсцисс отмечено девять точек: \(x_1, \, x_2, \, x_3,\, x_4, \, x_5,\, x_6,\, x_7, \,x_8,\,x_9.\) В скольких из этих точек производная функции \(y=f(x)\) положительна?
Посмотреть ответ Посмотреть решение
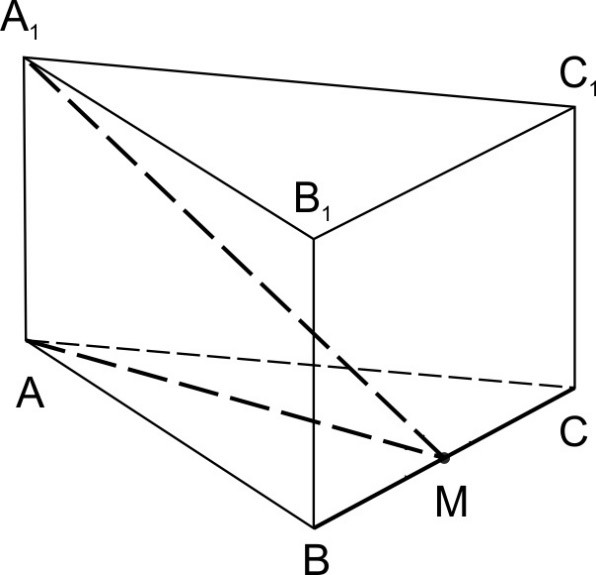
8. Анна Малкова Ребро основания правильной треугольной призмы \(ABCA_1B_1C_1\) равно \(\sqrt{12}\), боковое ребро равно 2,4. Точка М – середина ребра ВС. Найдите тангенс угла \(A_1MA. \)
Посмотреть ответ Посмотреть решение
9. Наталья Гаврилова
Вычислить:
\((5+ \sqrt3) \sqrt{28-10 \sqrt3}\)
Посмотреть ответ Посмотреть решение
10.
Высота над землей подброшенного вверх мяча меняется по закону
\(h(t)=-5 t^2+9 t+2 ,\) где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько процентов от времени всего полета мяч будет находиться на высоте не более 6 метров?
Посмотреть ответ Посмотреть решение
11. Анна Малкова
Мерлин задумал прокопать тайный подземный ход длиной 196 метров от своего дома до королевского замка. Бригада гномов берет 70 золотых за 1-й метр подземного хода и за каждый следующий метр на 14 золотых больше, чем за предыдущий. Также гномы требуют: по окончании работ выставить угощение для каждого гнома на сумму 80 золотых и выплатить каждому по 920 золотых премиальных. Бригада гоблинов просит 75 золотых за 1-й метр подземного хода и на 15 золотых больше за каждый следующий метр и ничего больше. Какое наибольшее количество гномов может быть в бригаде, чтобы Мерлину было выгоднее иметь дело с ними, а не с гоблинами?
Посмотреть ответ Посмотреть решение
12. Анна Малкова
Найдите наибольшее значение функции
\(y=2 \sqrt2 (sinx+cosx)\) на отрезке \([0; \pi ].\)
Посмотреть ответ Посмотреть решение
Часть 2. Задания с развернутым ответом
13.
а) Решить уравнение \(\displaystyle \frac{2-2 sin^2x- \sqrt3 cosx }{ctgx- \sqrt3} =0\)
б) найти все его корни на отрезке \([- \pi ;3 \pi ]\)
Посмотреть ответ Посмотреть решение
14. (ЕГЭ-2019) В правильной треугольной призме \(ABCA_1B_1C_1\) сторона основания равна 4, а боковое ребро равно 2. Точка M — середина ребра \(A_1C_1,\) а точка O — точка пересечения диагоналей боковой грани \(ABB_1A_1.\)
а) Докажите, что точка пересечения диагоналей четырёхугольника, являющегося сечением призмы \(ABCA_1B_1C_1\) плоскостью AMB лежит на отрезке \(OC_1.\)
б) Найдите угол между прямой \(OC_1,\) и плоскостью AMB.
Посмотреть ответ Посмотреть решение
15. Решить неравенство \(\displaystyle \frac{2}{5^{x+1}-1}+\frac{5^{x+1}-2}{5^{x+1}-3} \geq 2\)
Посмотреть ответ Посмотреть решение
16. Анна Малкова
На средней линии MN трапеции АВСD как на диаметре построена окружность с центром О, проходящая через вершины В и С верхнего основания трапеции и пересекающая нижнее основание АD в точках Р и Q, причем точка Р расположена между точками А и Q.
а) Докажите, что ВСQP – прямоугольник.
б) Найдите площадь четырехугольника АВОР, если AD = 12, высота трапеции АВСD равна 6.
Посмотреть ответ Посмотреть решение
17. Анна Малкова
1 сентября 2019 года в заповеднике обитало 256 криворогих оленей. Известно, что в течение года численность популяции криворогих оленей увеличивается в среднем на 25% (за счет естественного прироста). Кроме того, биологи собираются увеличить количество оленей в заповеднике не менее чем до 1000 и для этого 1 сентября 2020, 2021, 2022 и 2023 года будут завозить в заповедник одинаковое количество новых оленей. Какое наименьшее количество оленей им придется завозить в заповедник ежегодно?
Посмотреть ответ Посмотреть решение
18. Найдите все значения параметра а, для каждого из которых область значений функции \(\displaystyle y= \frac{sinx+a}{cos2x-2}\) содержит число 2.
Посмотреть ответ Посмотреть решение
19. В ящике лежит 76 фруктов, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два фрукта различной массы, а средняя масса всех фруктов равна 100 г. Средняя масса фруктов, масса каждого из которых меньше 100 г, равна 85 г. Средняя масса фруктов, масса каждого из которых больше 100 г, равна 124 г.
а) Могло ли в ящике оказаться поровну фруктов массой меньше 100 г и фруктов массой больше 100 г?
б) Могло ли в ящике оказаться меньше 8 фруктов, масса каждого из которых равна 100 г?
в) Какую наибольшую массу может иметь фрукт в этом ящике?