ОГЭ по Математике Вариант 1

1. Дан план участка.

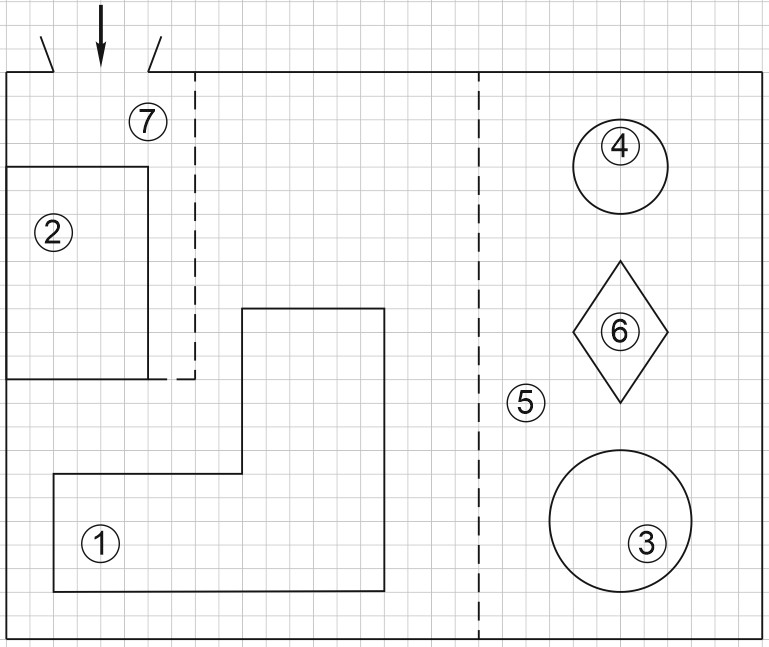
При входе на участок напротив ворот находится гараж, а за гаражом – жилой дом.

Площадь, занятая гаражом, равна 54 кв. м.

На газоне имеются круглый бассейн, беседка и ромбовидная клумба.

Беседка отмечена на плане цифрой 4.

При въезде на участок имеется площадка, вымощенная тротуарной плиткой с размером каждой плитки  \(0,2\) м \(\times 0,2\) м и обозначенная на плане цифрой 7.

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр.

Объекты	Жилой дом	Гараж	Бассейн	Клумба
Цифры

Посмотреть ответ. Посмотреть решение.

2. Дан план участка.

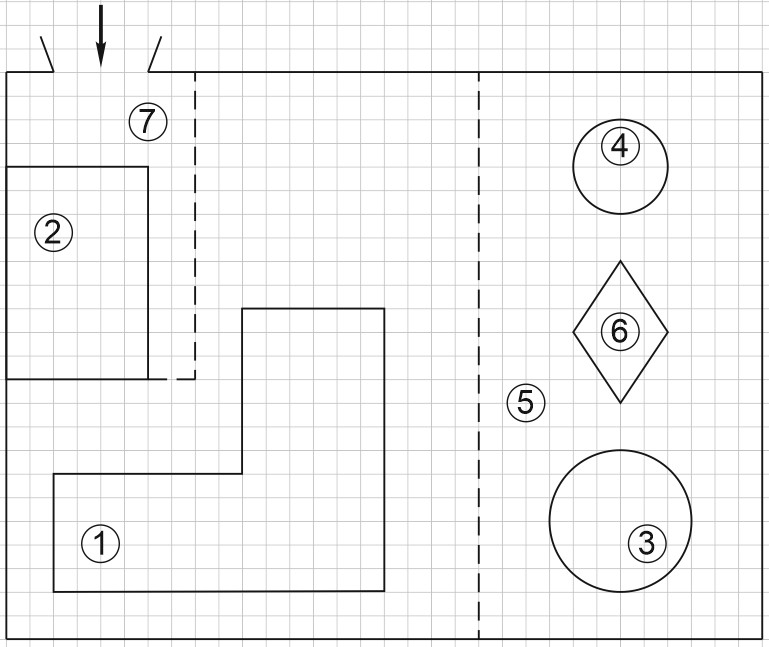
При входе на участок напротив ворот находится гараж, а за гаражом – жилой дом.

Площадь, занятая гаражом, равна 54 кв. м.

На газоне имеются круглый бассейн, беседка и ромбовидная клумба.

Беседка отмечена на плане цифрой 4.

При въезде на участок имеется площадка, вымощенная тротуарной плиткой с размером каждой плитки  \(0,2\) м \(\times 0,2\) м и обозначенная на плане цифрой 7.

Найдите площадь, которую занимает клумба. Ответ дайте в квадратных метрах.

Посмотреть ответ. Посмотреть решение.

3. Дан план участка.

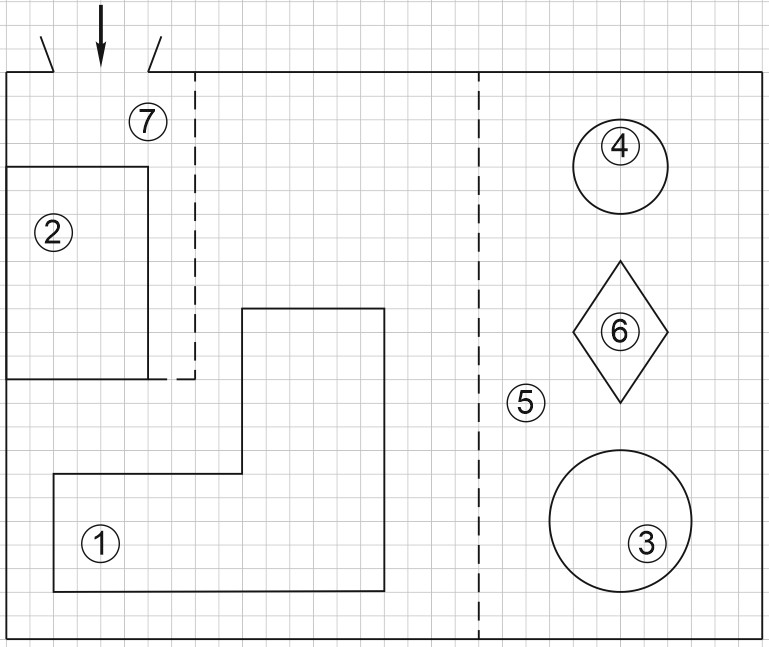
При входе на участок напротив ворот находится гараж, а за гаражом – жилой дом.

Площадь, занятая гаражом, равна 54 кв. м.

На газоне имеются круглый бассейн, беседка и ромбовидная клумба.

Беседка отмечена на плане цифрой 4.

При въезде на участок имеется площадка, вымощенная тротуарной плиткой с размером каждой плитки  \(0,2\) м \(\times 0,2\) м и обозначенная на плане цифрой 7.

Тротуарная плитка продаётся в упаковках по 45 штук. Сколько упаковок плитки понадобилось, чтобы выложить площадку перед гаражом?

Посмотреть ответ. Посмотреть решение.

4. Дан план участка.

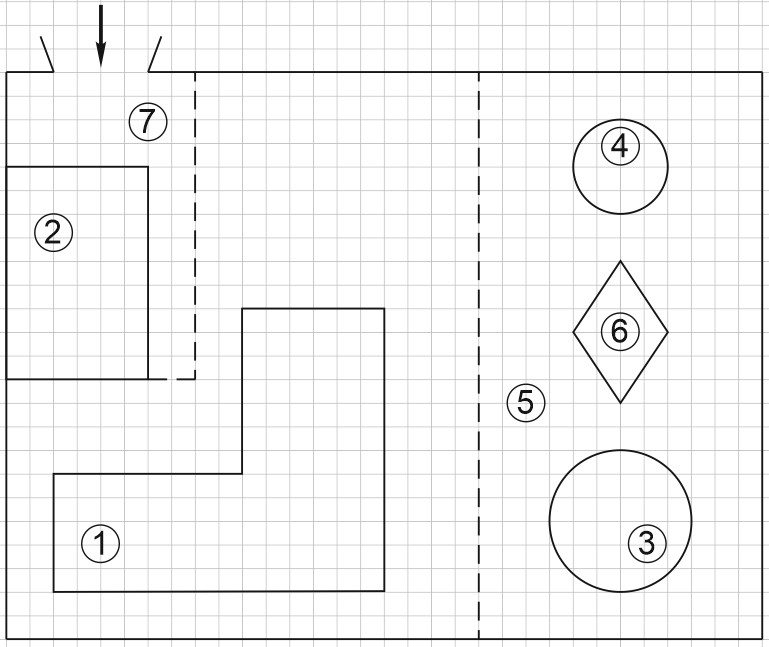
При входе на участок напротив ворот находится гараж, а за гаражом – жилой дом.

Площадь, занятая гаражом, равна 54 кв. м.

На газоне имеются круглый бассейн, беседка и ромбовидная клумба.

Беседка отмечена на плане цифрой 4.

При въезде на участок имеется площадка, вымощенная тротуарной плиткой с размером каждой плитки  \(0,2\) м \(\times 0,2\) м и обозначенная на плане цифрой 7.

Во сколько раз площадь бассейна больше площади беседки?

Посмотреть ответ. Посмотреть решение.

5. Дан план участка.

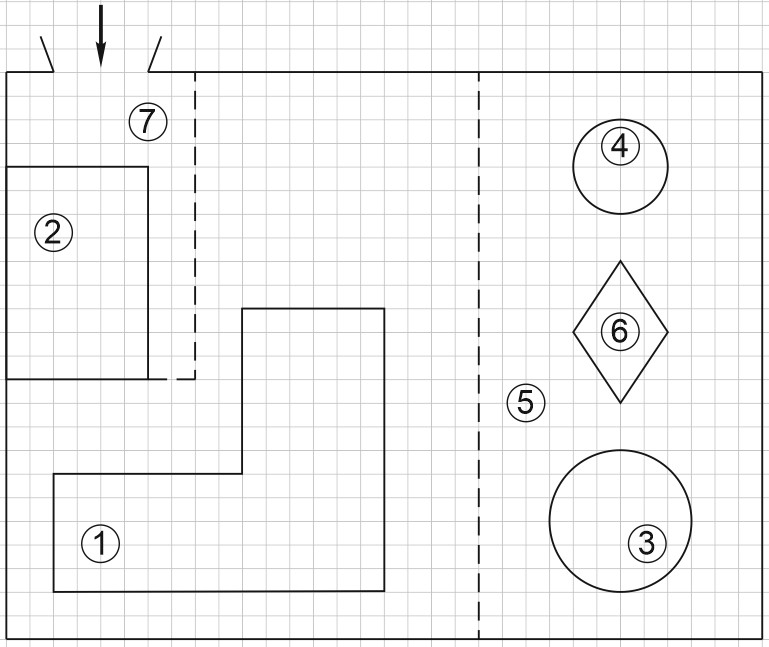
При входе на участок напротив ворот находится гараж, а за гаражом – жилой дом.

Площадь, занятая гаражом, равна 54 кв. м.

На газоне имеются круглый бассейн, беседка и ромбовидная клумба.

Беседка отмечена на плане цифрой 4.

При въезде на участок имеется площадка, вымощенная тротуарной плиткой с размером каждой плитки  \(0,2\) м \(\times 0,2\) м и обозначенная на плане цифрой 7.

Хозяин участка хочет обновить газон к новому дачному сезону. Для этого он планирует купить семена газонной травы. Цена одной упаковки семян, её масса и рекомендуемый расход указаны в таблице.

Во сколько рублей обойдётся наиболее дешёвый вариант? (Территорию, занятую бассейном и беседкой, засевать не предполагается. Клумбу планируется убрать, и на её место тоже засеять газонную траву. Число  возьмите равным 3. Считаем, что все купленные семена - одного сорта).

Поставщик	Цена 1 уп. семян (руб.)	Масса 1 уп. семян (кг.)	Рекомендуемый расход 1 уп. семян (кв. м.)
А	520	1,5	60
Б	350	1,2	40
В	330	1	35
Г	400	1	45

Посмотреть ответ. Посмотреть решение.

6. Найдите значение выражения: \(6\cdot\left (\displaystyle \frac{1}{3}\right )^2-11\cdot \displaystyle \frac{1}{3}.\)

Посмотреть ответ. Посмотреть решение.

7. На координатной прямой отмечено число \(a.\)

Расположите в порядке возрастания числа \(a-1, \ \displaystyle \frac{1}{a}, \ a.\)

В ответе укажите номер правильного варианта.

1) \(a, \ \displaystyle \frac{1}{a}, \ a-1.\)

2) \(a, \ a-1,\ \displaystyle \frac{1}{a}.\)

3) \(a-1, \ a, \ \displaystyle \frac{1}{a}.\)

4) \(\displaystyle \frac{1}{a}, \ a-1, \ a.\)

Посмотреть ответ. Посмотреть решение.

8. Найдите значение выражения: \(\displaystyle \frac{1}{\sqrt{10}-3}-\frac{1}{\sqrt{10}+3}.\)

Посмотреть ответ. Посмотреть решение.

9. Решите систему уравнений: \(\left\{\begin{matrix}
3x-y=-1, \\
-x+2y=7.\end{matrix}\right.\) В ответе запишите через точку с запятой без пробелов пару чисел \(x; y.\) Например: \(7;9\)

Посмотреть ответ. Посмотреть решение.

10. Игральную кость бросают дважды. Найдите вероятность того, что наименьшее из двух выпавших чисел равно 2 или оба числа равны 2.

Посмотреть ответ. Посмотреть решение.

11. Установите соответствие между функциями и их графиками.

Функции:

А) \(y=\displaystyle \frac{1}{4x};\)

Б) \(y=3x^2-9x+6;\)

В) \(y=4x+5.\)

Графики:

Запишите по порядку номера графиков, соответствующих функциям в пунктах А, Б и В.

Посмотреть ответ. Посмотреть решение.

12. Чтобы перевести значение температуры по шкале Цельсия \( (t^{\circ}C)\) в шкалу Фаренгейта \( (t^{\circ}F)\), пользуются формулой \(F = 1,8C+32\), где \(C\) — градусы Цельсия, \(F\)   — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует \(158^{\circ}\) по шкале Фаренгейта?

Посмотреть ответ. Посмотреть решение.

13. На каком рисунке изображено множество решений системы неравенств \(\left\{\begin{matrix}
x<3, \\ 4-x>0.\end{matrix}\right.\)?

В ответе укажите номер правильного варианта.

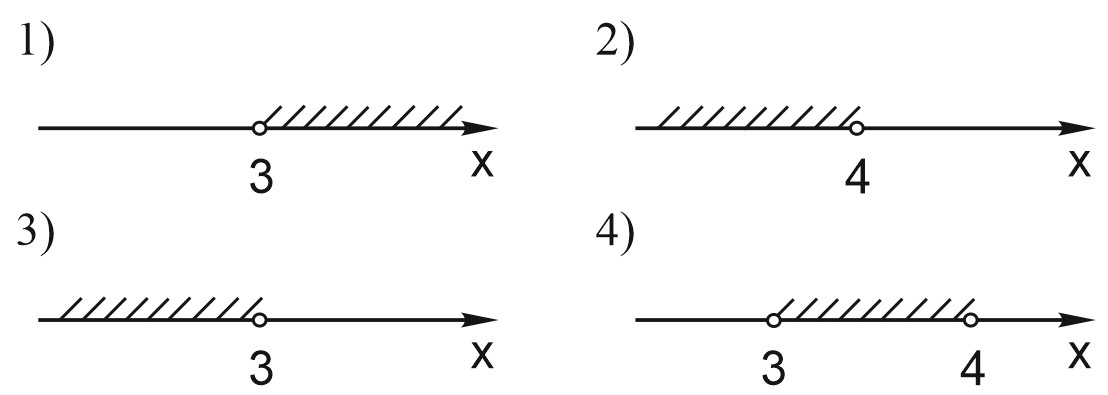
Посмотреть ответ. Посмотреть решение.

14. Футбольный мяч катится так, что за первую секунду он проходит путь 0,6 м, а в каждую следующую секунду путь увеличивается на 0,6 м по сравнению с предыдущей. Сколько секунд будет катиться мяч по горке длиной 6 метров?

Посмотреть ответ. Посмотреть решение.

15. В треугольнике \(ABC\) угол \(ACB\) равен \(90^{\circ}\), угол \(B\) равен \(58^{\circ}, \ CD\) — медиана. Найдите угол \(ACD.\) Ответ дайте в градусах.

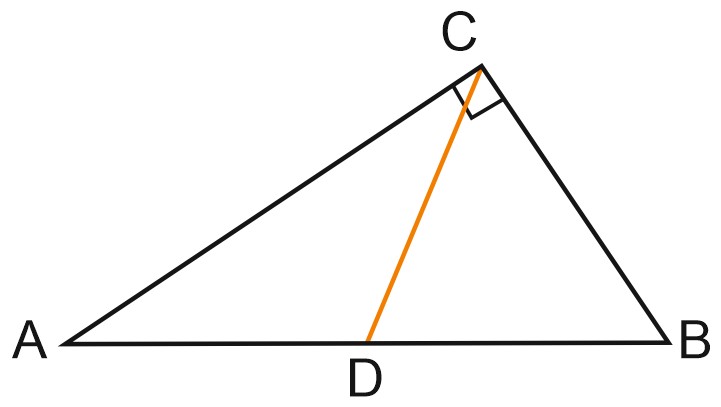
Посмотреть ответ. Посмотреть решение.

16. Найдите вписанный угол, опирающийся на дугу, равную \(\displaystyle \frac{1}{5}\) окружности. Ответ дайте в градусах.

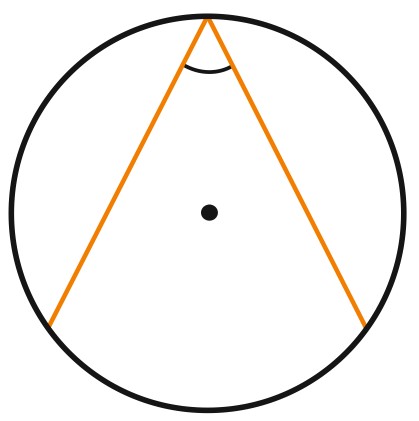
Посмотреть ответ. Посмотреть решение.

17. Площадь параллелограмма \(ABCD\) равна 3. Точка \(H\) — середина стороны \(AD.\) Найдите площадь трапеции \(AHCB.\)

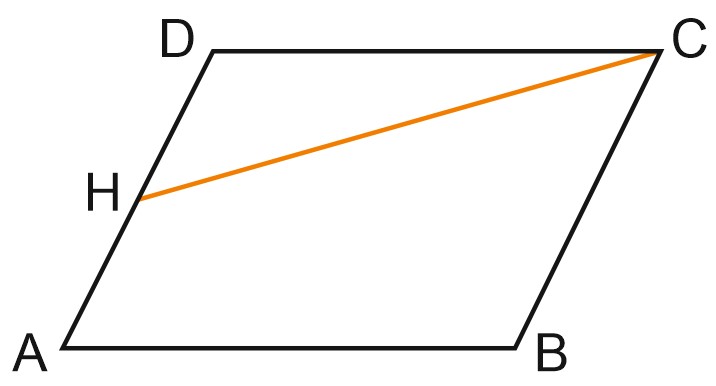
Посмотреть ответ. Посмотреть решение.

18. Найдите угол \(ABC.\) Ответ дайте в градусах.

Посмотреть ответ. Посмотреть решение.

19. Какие из следующих утверждений верны?

1)  В треугольнике против меньшего угла лежит большая сторона.

2)  Если один угол треугольника больше \(120^{\circ}\), то два других его угла меньше \(30^{\circ}.\)

3)  Если все стороны треугольника меньше 1, то и все его высоты меньше 1.

4)  Сумма острых углов прямоугольного треугольника не превосходит \(90^{\circ}.\)

Посмотреть ответ. Посмотреть решение.

20. Решите уравнение: \(x^4-2x^2-15=0.\) В ответе запишите произведение корней.

Посмотреть ответ. Посмотреть решение.

21. Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?

Посмотреть ответ. Посмотреть решение.

22. Известно, что графики функций \(y=x^2+p\) и \(y=-2x-5\) имеют ровно одну общую точку. Определите координаты этой точки. В ответе запишите координаты этой точки \(x; y.\) без пробелов.

Постройте графики заданных функций в одной системе координат.

Посмотреть ответ. Посмотреть решение.

23. Около окружности описана прямоугольная трапеция, периметр которой равен 32, а большая боковая сторона равна 10. Определите, на сколько одно основание трапеции больше другого.

Посмотреть ответ. Посмотреть решение.

24. В остроугольном треугольнике \(ABC\) угол \(B\) равен \(60^{\circ}.\) Докажите, что точки \(A, \ C\), центр описанной окружности треугольника \(ABC\) и точка пересечения высот треугольника \(ABC\) лежат на одной окружности.

Каким из полезных фактов вы пользовались при доказательстве? Выберите правильный вариант. В ответе запишите (без точки) номер этого варианта, например: 1

1) Три высоты треугольника пересекаются в одной точке.

2) Вписанный угол равен половине центрального, опирающегося на ту же дугу.

3) Площадь треугольника равна половине произведения основания на высоту.

Посмотреть ответ. Посмотреть решение.

25. В параллелограмме \(ABCD\) проведена диагональ \(AC.\) Точка \(O\) является центром окружности, вписанной в треугольник \(ABC.\) Расстояния от точки \(O\) до точки \(A\) и прямых \(AD\) и \(AC\) соответственно равны 5, 4 и 3. Найдите площадь параллелограмма \(ABCD.\)

Посмотреть ответ. Посмотреть решение.