Часть 1. Задания с кратким ответом
1. Программист Егор получает 96000 рублей в месяц. Егор решил ежемесячно откладывать 25% заработной платы на покупку квартиры, стоимость которой составляет 3600000 рублей. Какое наименьшее целое количество лет необходимо для покупки квартиры, если бы зарплата Егора и стоимость квартиры оставались постоянными?
Посмотреть ответ Посмотреть решение
2. Наталья Гаврилова, Ярославль
На рисунке жирными точками показаны продажи холодильников магазином бытовой техники в течение года (для наглядности точки соединены линией). По горизонтали указан номер месяца, а по вертикали – количество проданных в этом месяце холодильников. Определите по рисунку, во сколько раз больше было продано холодильников в летние месяцы, чем в зимние.
Посмотреть ответ Посмотреть решение
3. Найдите площадь многоугольника АВСDE, изображенного на рисунке.
Посмотреть ответ Посмотреть решение
4. Дарья Тиунель, Беларусь. Ведущий конкурса предлагает троим участникам задумать любую цифру от 0 до 9. Считая, что выбор каждым из участников любой цифры равновероятен, найти вероятность того, что у кого-то из них задуманные цифры совпадут.
Посмотреть ответ Посмотреть решение
5. Наталья Гаврилова. Решить уравнение: \((10x-2)\cdot \sqrt{x-6}=0.\)
Если уравнение имеет более одного корня, в ответе укажите меньший корень.
Посмотреть ответ Посмотреть решение
6. Угол между медианой и высотой прямоугольного треугольника АВС, проведенными из вершины прямого угла, равен 38 градусов. Найдите меньший из углов треугольника АВС. Ответ выразите в градусах.
Посмотреть ответ Посмотреть решение
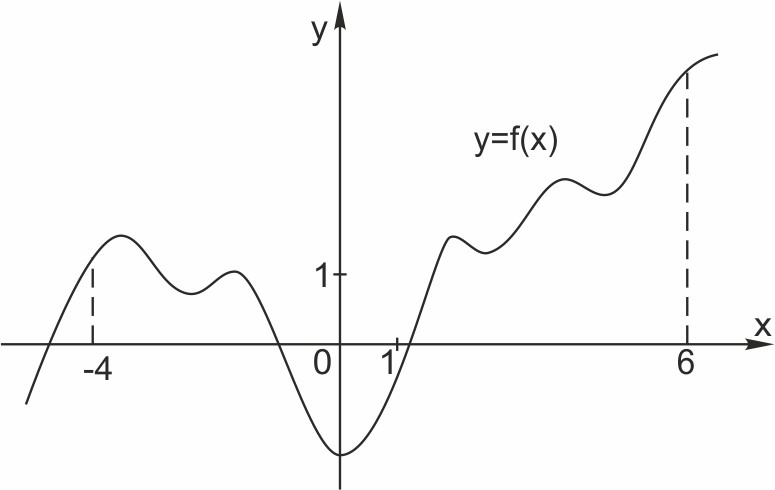
7. На рисунке изображен график непрерывной функции у = f(x). Найдите количество точек максимума функции на отрезке [ - 4; 6 ].
Посмотреть ответ Посмотреть решение
8. Найдите объем восьмигранника, изображенного на рисунке, если АВСD – квадрат со стороной 5, О – точка пересечения его диагоналей, отрезок EF перпендикулярен плоскости АВС, ОЕ = ОF = 6.
Посмотреть ответ Посмотреть решение
9. Наталья Гаврилова.
Вычислить \(\displaystyle \frac{153^3-1}{153^2+153+1}\)
Посмотреть ответ Посмотреть решение
10. Наталья Гаврилова
Тормозной путь автомобиля можно вычислить по формуле \(\displaystyle S=\frac{v_0^2}{2g\cdot \mu}\) , где S – тормозной путь в метрах, \(v_0\) – скорость движения автомобиля в момент начала торможения в м/с, g – ускорение свободного падения, равное 9,8 м/с², \(\mu\) – коэффициент сцепления шин с дорогой. Определить с какой скоростью двигался автомобиль в момент начала торможения, если его тормозной путь равен 20 м, а коэффициент сцепления шин с сухим асфальтобетонным покрытием равен 0,72. Ответ дайте в км/ч.
Посмотреть ответ Посмотреть решение
11. Два автомобиля, двигаясь по кольцевой дороге с постоянными скоростями в одном направлении, оказываются рядом через каждые 3 ч. При движении с теми же скоростями в противоположных направлениях автомобили встречаются через каждые 20 мин. Найдите, за какое время в минутах проезжает всю трассу автомобиль, двигающийся с большей скоростью.
Посмотреть ответ Посмотреть решение
12. Найдите наибольшее значение функции
\(y=-x^2+10x-24\)
на отрезке [4,2; 4,5]
Посмотреть ответ Посмотреть решение
Часть 2. Задания с развернутым ответом
13. а) Решить уравнение \(2 cos^2x+5 sinx=5\)
б) найти корни, принадлежащие отрезку \(\displaystyle [-\frac{\pi}{2};2\pi]\)
Посмотреть ответ Посмотреть решение
14. Анна Малкова.
В правильной четырехугольной пирамиде SABCD сторона основания АВ = 12, высота SO = 15, точка М лежит на отрезке АС, АМ : МС = 7 : 5.
а) Постройте сечение пирамиды плоскостью, проходящей через точку М перпендикулярно прямой АС.
б) Найдите площадь сечения.
Посмотреть ответ Посмотреть решение
15. Решите неравенство \(\displaystyle \frac{x^2-3x-5}{x-4}+\frac{3x^2-15x+2}{x-5} \leq 4x+1\)
Посмотреть ответ Посмотреть решение
16. Татьяна Щетинина.
В параллелограмме ABCD угол А равен \(60^\circ, \, AB=6, \, AD=10.\) На лучах AD и СD отмечены точки М и К соответственно, причём СМ=СD и АК=АD.
а) Докажите, что точки А, В, С, М и К лежат на одной окружности
б) Найдите площадь треугольника КМВ
Посмотреть ответ Посмотреть решение
17. Анна Малкова
Программист Егор решил, что не будет копить, а купит квартиру в ипотеку под 25% годовых. Егор рассчитал, что если выплачивать кредит ежегодными платежами, составляющими 738 тысяч рублей, кредит будет полностью выплачен за 3 года. Какими должны быть ежегодные платежи, чтобы Егор смог выплатить ипотечный кредит за 4 года? Ответ дайте в тысячах рублей.
Посмотреть ответ Посмотреть решение
18. При каких значениях параметра а система двух уравнений
\(\left\{\begin{gathered}(a+1)x+8y=4a \\ ax+(a+3)y=3a-1 \end{gathered}\right.\)
имеет бесконечно много решений?
Посмотреть ответ Посмотреть решение
19. Антон Акимов, Москва
Петя написал на доске числа 1, 2, 3, 4 и подвёл к ней робота-
математика Константина. Каждую минуту Константин проводит операцию:
стирает с доски какие-нибудь три числа a, b, c и записывает вместо них числа \(\displaystyle \frac{ab}{c}, \frac{bc}{a}, \frac{ca}{b}\)
а) Могут ли после нескольких операций на доске остаться только числа,
большие 1?
б) Может ли через некоторое время на доске оказаться натуральное число,
большее 100?
в) Известно, что после нескольких операций на доске оказались числа \(\displaystyle \frac{1}{4}, 6, \frac{27}{2}\) и ещё одно. Какое?
Посмотреть ответ Посмотреть решение