Часть 1. Задания с кратким ответом
1. В 11 «А» классе 27 учеников, причем девочек на 25% больше, чем мальчиков. Сколько девочек в 11 «А»?
Посмотреть ответ Посмотреть решение
2. На рисунке представлен график зависимости силы тока (в амперах) в проводнике от его сопротивления (в омах). По графику определите силу тока при сопротивлении 5 Ом. Ответ выразите в амперах.
Посмотреть ответ Посмотреть решение
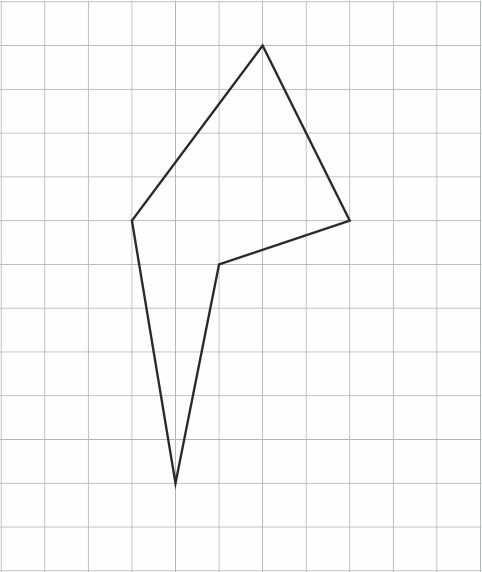
3. Найдите площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах.
Посмотреть ответ Посмотреть решение
4. Известно, что в семье Ивановых четверо детей. Найдите вероятность того, что ровно трое из четырех детей – девочки.
Посмотреть ответ Посмотреть решение
5. Решите уравнение:
\(log_2 \, ^2\, x+log_2x=0\)
Если уравнение имеет несколько корней, в ответе запишите меньший корень.
Посмотреть ответ Посмотреть решение
6. Прямая, параллельная основаниям АD и ВС трапеции АВСD и проходящая через точку пересечения ее диагоналей, пересекает боковые стороны трапеции в точках М и N. Найдите МN, если AD = 7, BC = 3.
Посмотреть ответ Посмотреть решение
7. На рисунке изображен график \(y=f' (x)\) — производной непрерывной функции
\(y=f (x).\) В какой точке функция \(y=f (x)\) принимает наименьшее значение?
Посмотреть ответ Посмотреть решение
8. Найдите объем детали, изображенной на рисунке, если диаметр основания цилиндра равен 10, высота равна \(\displaystyle \frac{4} {\pi},\) а диаметр цилиндрического отверстия равен 4.
Посмотреть ответ Посмотреть решение
9. Найдите значение выражения:
\(\displaystyle \frac{1}{2} + sin \frac{\pi}{12} \, sin \frac{5\pi}{12} - sin^2 \frac{\pi}{3}\)
Посмотреть ответ Посмотреть решение
10. При параллельном соединении резисторов с сопротивлениями \(R_1\) и \(R_2\) общее сопротивление R рассчитывается по формуле \(\displaystyle \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}.\) Сопротивление \(R_1\) можно изменять в пределах от 120 до 200 Ом, а сопротивление \(R_2\) в пределах от 600 до 720 Ом. Найдите наименьшее возможное значение сопротивления \(R_1,\) при котором общее сопротивление участка цепи равно 120 Ом. Ответ выразите в Омах.
Посмотреть ответ Посмотреть решение
11. Анна Малкова. Из пункта А выехал автомобиль «Ока». В тот же момент из пункта В навстречу ему выехал автомобиль «Пежо» со скоростью на 35 км/ч большей, чем у «Оки», и через 5 часов проехал мимо «Оки». Через час после выезда «Оки» из пункта А стартовал автомобиль «Лада Калина» со скоростью на 4 км/ч большей, чем у «Оки», и достиг пункта В одновременно с «Окой». Найдите скорость автомобиля «Ока». Ответ выразите в км/ч.
Посмотреть ответ Посмотреть решение
12. Найдите наименьшее значение функции \(y=3 cosx- \pi x+ \pi ^2\) на отрезке \([-2 \pi ; \pi ].\)
Посмотреть ответ Посмотреть решение
Часть 2. Задания с развернутым ответом
13. а) Решите уравнение: \(\displaystyle \frac{1}{sinx} + \frac{1}{cosx} =2\sqrt 2\)
б) Найдите все корни уравнения на отрезке \([\displaystyle \frac{- \pi}{3}; \pi ]\)
Посмотреть ответ Посмотреть решение
14. Анна Малкова. В треугольной пирамиде SABC все плоские углы при вершине S – прямые, длины ребер SА, SВ и SС равны\(\sqrt {\sqrt 5+\sqrt 3} , \, \, \sqrt {\sqrt 5-\sqrt 3}\) и \(6\sqrt 2\) соответственно. Плоскость \(\alpha \) проходит через середины ребер SA, SC и ВС.
а) Докажите, что сечение пирамиды плоскостью \(\alpha\) является прямоугольником.
б) Найдите объем пирамиды с вершиной S, основанием которой является сечение пирамиды SABC плоскостью \(\alpha .\)
Посмотреть ответ Посмотреть решение
15. Решите неравенство: \(\sqrt {log_3x } + 2\sqrt {log_x3 } \geq 3\)
Посмотреть ответ Посмотреть решение
16. Антон Акимов В трапеции ABCD точки M и N — середины боковых сторон AB и CD соответственно. Известно, что AD = 14, CM = 5, AN = 5, а высота трапеции равна 8.
а) Докажите, что около трапеции ABCD нельзя описать окружность.
б) Известно, что \(AD \, \textgreater \, BC.\) Найдите площадь трапеции ABCD.
Посмотреть ответ Посмотреть решение
17. Анна Малкова 15-го января 2018 года Роман взял в банке кредит на сумму 5 020 000 рублей на срок 24 месяца.
Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму Роман вернёт банку в течение трех летних месяцев 2018 года?
Посмотреть ответ Посмотреть решение
18. Анна Малкова
При каких значениях параметра а уравнение
\(\sqrt {x^2-4ax+4a^2 }-\sqrt {x^2+6ax+9a^2 }=4 sinx \)
имеет бесконечно много решений?
Посмотреть ответ Посмотреть решение
19. В коробке находятся 13 красных и 17 белых фишек; есть также неограниченное число фишек того и другого цвета. Разрешается совершать в любом порядке и в любом количестве следующие действия:
1) Увеличить на 2 число красных фишек и одновременно уменьшить на 1 число белых,
2) Увеличить на 1 число красных фишек и одновременно увеличить на 2 число белых,
3) Уменьшить на 2 число красных фишек и одновременно увеличить на 1 число белых,
4) Уменьшить на 1 число красных фишек и одновременно уменьшить на 2 число белых,
а) Может ли в коробке в результате 8 действий остаться ровно 30 фишек?
б) Может ли в результате некоторого числа действий получиться 37 красных и 43 белых фишек?
в) Какое наименьшее число фишек может получиться?
Посмотреть ответ Посмотреть решение